A circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AEB
The correct Answer is:27∘
To solve the problem step by step, we need to analyze the given information about the pentagon ABCDE and the angles involved.
Step 1: Understand the given information
We know that:
- A circle with center O circumscribes the pentagon ABCDE.
- AB−BC=CD
- ∠BCD=126∘
Step 2: Establish relationships in triangles
Since O is the center of the circle, the segments OB, OC, and OD are radii of the circle. Therefore:
- OB=OC=OD
Step 3: Analyze triangle BOC and COD
From the information given:
- AB−BC=CD implies BC=AB−CD.
- We can also see that triangles BOC and COD share side OC.
Step 4: Use the angle BCD to find angles OCB and OCD
By the property of angles in a circle, we have:
- ∠OCB=∠OCD=12∠BCD
- Substituting the value of ∠BCD:
∠OCB=∠OCD=12×126∘=63∘
Step 5: Find angle OBC
In triangle BOC, since OB = OC (radii of the circle), we have:
- ∠OCB=∠OBC
- Therefore, ∠OBC=63∘.
Step 6: Use the angle sum property in triangle BOC
The sum of angles in triangle BOC is:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
63∘+63∘+∠BOC=180∘
This simplifies to:
∠BOC=180∘−126∘=54∘
Step 7: Find angle AOB
Since AB=BC=CD, we can conclude:
- ∠AOB=∠BOC=∠COD=54∘.
Step 8: Find angle AEB
Using the property that the angle subtended by an arc at any point on the circumference is half the angle subtended at the center:
∠AEB=12∠AOB
Substituting the value of ∠AOB:
∠AEB=12×54∘=27∘
Final Answer
Thus, the measure of angle AEB is:
∠AEB=27∘
We know that:
- A circle with center O circumscribes the pentagon ABCDE.
- AB−BC=CD
- ∠BCD=126∘
Since O is the center of the circle, the segments OB, OC, and OD are radii of the circle. Therefore:
- OB=OC=OD
From the information given:
- AB−BC=CD implies BC=AB−CD.
- We can also see that triangles BOC and COD share side OC.
By the property of angles in a circle, we have:
- ∠OCB=∠OCD=12∠BCD
- Substituting the value of ∠BCD:
∠OCB=∠OCD=12×126∘=63∘
In triangle BOC, since OB = OC (radii of the circle), we have:
- ∠OCB=∠OBC
- Therefore, ∠OBC=63∘.
The sum of angles in triangle BOC is:
∠OBC+∠OCB+∠BOC=180∘
Substituting the known values:
63∘+63∘+∠BOC=180∘
This simplifies to:
∠BOC=180∘−126∘=54∘
Since AB=BC=CD, we can conclude:
- ∠AOB=∠BOC=∠COD=54∘.
Using the property that the angle subtended by an arc at any point on the circumference is half the angle subtended at the center:
∠AEB=12∠AOB
Substituting the value of ∠AOB:
∠AEB=12×54∘=27∘
Thus, the measure of angle AEB is:
∠AEB=27∘
Topper's Solved these Questions
Similar Questions
A circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AOC
View SolutionA circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AED
View SolutionABCDE is a cyclic pentagon with centre of its circumcircle alt point O such that AB=BC=CD and angle ABC=120∘
Calculate
(i) ∠BEC (ii) ∠BED
View SolutionIn cyclic quadrilateral ABCD , AD = BC, ∠BAC=30∘and∠CBD=70∘ , find : angle ADC .
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠ABC
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
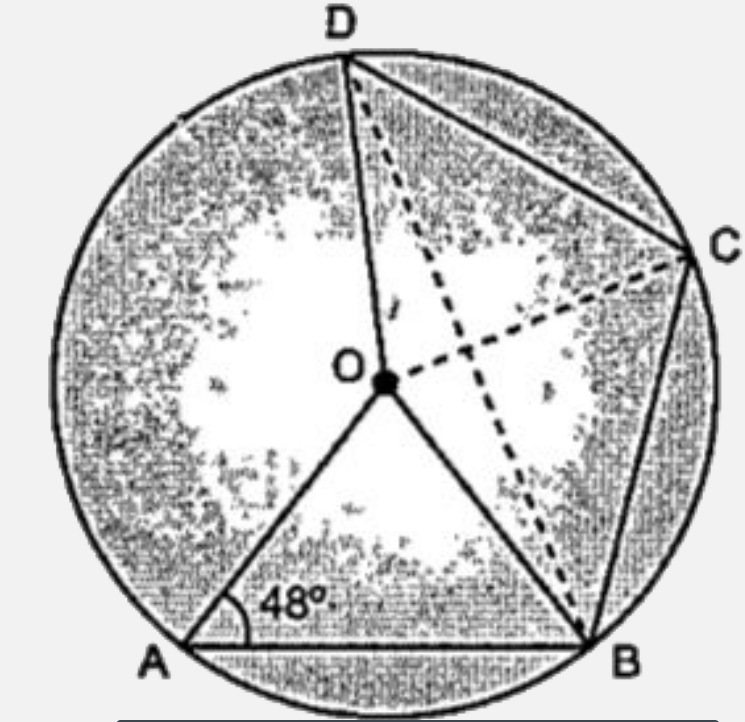
∠OBD
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCD
View SolutionIn cyclic quadrilateral ABCD , AD = BC ,∠BAC=30∘and∠CBD=70∘ , find :
∠BCA
View SolutionIn the given below AB is parallel to CD and CA = CE .
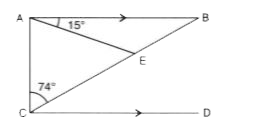
If angle ACE = 74∘and∠EAB=15∘ find the angles AEB and BCD.
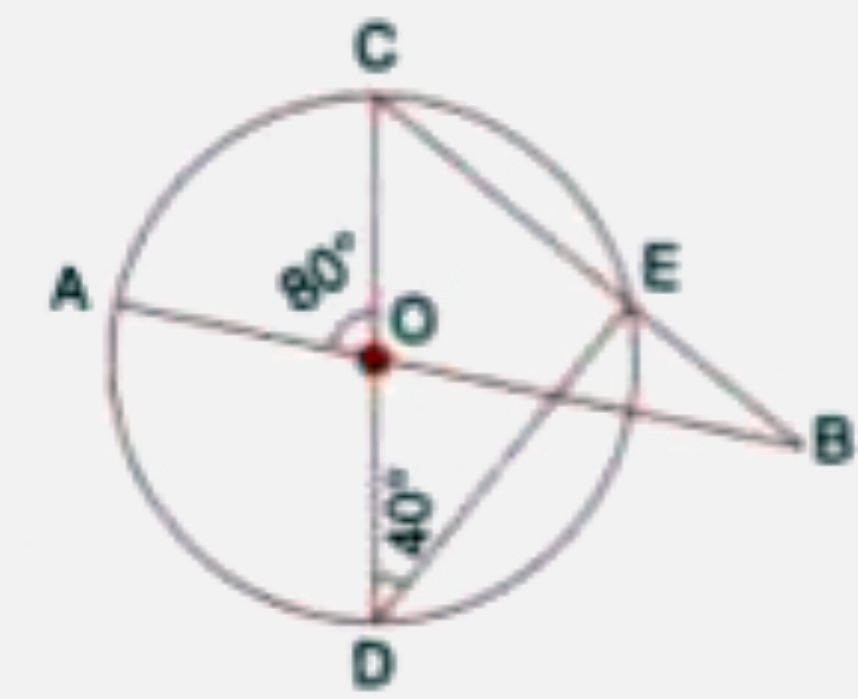
View SolutionIn the figure given alongside ,AB and CD are straight lines thorugh the centre O of a circle. If ∠AOC=80∘and∠CDE=40∘ , find ∠DCE
View Solution
