Find the range of vaues of x, which satisfy the inequality :
−15≤3x10+1<25,x∈R.
Graph the solution set on the number line.
The correct Answer is:30∘
To solve the inequality −15≤3x10+1<25, we will break it down into two parts and solve each part step by step.
Step 1: Break down the inequality
We can rewrite the compound inequality as two separate inequalities:
1. −15≤3x10+1
2. 3x10+1<25
Step 2: Solve the first inequality
Starting with the first inequality:
−15≤3x10+1
Subtract 1 from both sides:
−15−1≤3x10
Convert 1 to a fraction with a denominator of 5:
−15−55=−65
So we have:
−65≤3x10
Now, multiply both sides by 10 to eliminate the fraction:
10⋅−65≤3x
This simplifies to:
−12≤3x
Now, divide both sides by 3:
−4≤xorx≥−4
Step 3: Solve the second inequality
Now, we will solve the second inequality:
3x10+1<25
Subtract 1 from both sides:
3x10<25−1
Convert 1 to a fraction with a denominator of 5:
25−55=−35
So we have:
3x10<−35
Now, multiply both sides by 10:
3x<10⋅−35
This simplifies to:
3x<−6
Now, divide both sides by 3:
x<−2
Step 4: Combine the results
From the two inequalities, we have:
1. x≥−4
2. x<−2
Combining these gives us:
−4≤x<−2
Step 5: Write the final answer
The range of values of x that satisfy the inequality is:
x∈(−4,−2)
Step 6: Graph the solution set on the number line
To represent this on a number line:
- Mark the point −4 with a closed dot (indicating that −4 is included).
- Mark the point −2 with an open dot (indicating that −2 is not included).
- Shade the region between −4 and −2.
We can rewrite the compound inequality as two separate inequalities:
1. −15≤3x10+1
2. 3x10+1<25
Starting with the first inequality:
−15≤3x10+1
Subtract 1 from both sides:
−15−1≤3x10
Convert 1 to a fraction with a denominator of 5:
−15−55=−65
So we have:
−65≤3x10
Now, multiply both sides by 10 to eliminate the fraction:
10⋅−65≤3x
This simplifies to:
−12≤3x
Now, divide both sides by 3:
−4≤xorx≥−4
Now, we will solve the second inequality:
3x10+1<25
Subtract 1 from both sides:
3x10<25−1
Convert 1 to a fraction with a denominator of 5:
25−55=−35
So we have:
3x10<−35
Now, multiply both sides by 10:
3x<10⋅−35
This simplifies to:
3x<−6
Now, divide both sides by 3:
x<−2
From the two inequalities, we have:
1. x≥−4
2. x<−2
−4≤x<−2
The range of values of x that satisfy the inequality is:
x∈(−4,−2)
To represent this on a number line:
- Mark the point −4 with a closed dot (indicating that −4 is included).
- Mark the point −2 with an open dot (indicating that −2 is not included).
- Shade the region between −4 and −2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If x2−5≤x3−4,x∈R, then the solution set of x on the number line is:
A B
B C
C D
D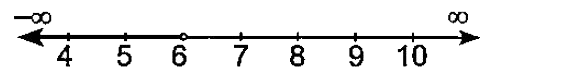
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A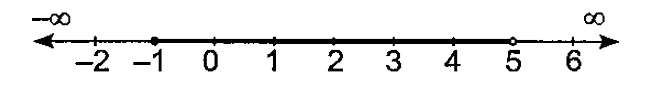 B
B C
C D
D
If 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
A B
B C
C D
D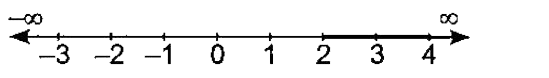
Find the values of x, which satisfy the inequation:
−2≤12−2x3≤156,x∈N.
Graph the solution on the number line.
View SolutionFind the values of x which satisfy the inequality −3<2x−1<19 .
View SolutionSolve the inequation :
−212+2x≤4x5≤43+2x,x∈W.
Graph the solution set on the number line.
View SolutionSimplify : - 13≤x2−113<16:x∈R.
Graph the values of x on the real number line.
View SolutionIf 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
View Solution
