ABCDE is a cyclic pentagon with centre of its circumcircle alt point O such that AB=BC=CD and angle ABC=120∘
Calculate
(i) ∠BEC (ii) ∠BED
The correct Answer is:(i) 30∘(ii)60∘
Step by step video, text & image solution for ABCDE is a cyclic pentagon with centre of its circumcircle alt point O such that AB=BC=CD and angle ABC=120^(@) Calculate (i) /_BEC (ii) /_BED by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)18videos
TANGENTS AND INTERSECTING CHORDS
- BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C12videos
SPECIMEN QUESTION PAPER (MATHEMATICS)
- BOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS22videos
TRIGONOMETRICAL IDENTITIES
Similar Questions
A circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AEBView SolutionA circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AEDView SolutionA circle, with centre O, circumscribs a pentagon ABCDE. IF AB−BC=CDand∠BCD=126∘, find:
∠AOCView SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED
 View Solution
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠BICView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠BCDView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:

∠CBDView SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
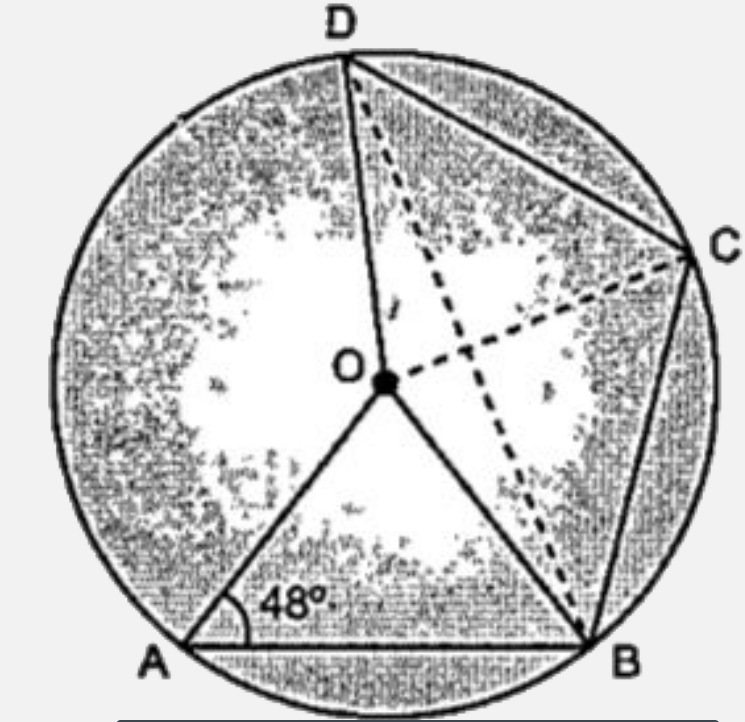
∠OBDView SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:

∠DCIView SolutionIn the followoing figure , AD is the diameter of the circle with centre O. Chords AB,BC and CD are equal .If ∠DEF=110∘, Calculate :
(i) ∠AEF.
(ii) ∠FAB
(##SEL_RKB_ICSE_MAT_X_C17_E03_002_Q01.png" width="80%">View Solution

