LC Oscillation
Step by step video solution for LC Oscillation by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A 1.5 μF capacitor is charged to 57V. The charging battery is then disconnected, and a 12 mH coil is connected in series with the capacitor so that LC Oscillations occur. What is the maximum current in the coil? Assume that the circuit has no resistance.
View SolutionA 10μF capacitor is charged to a potential of 25 V. The battery is then disconnected and a pure 100 mH coil is connected across the capacitor so that LC oscillations are set-up. What is the maximum current in the coil ?
View Solution
Knowledge Check
A 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write current in the inductor as a function of time
Al=(0.2A)sinωtBl=(0.3A)sinωtCl=(0.5A)sinωtDNone of the AboveA 16 μF capacitor is charged to a 20 Volt potential. Battery is then disconnected and inductor of inductance 40mH is connected across the capacitor, So that LC oscillations are step-up. Maximum current in the coil is
A0.4 AB2AC0.8 AD0.2 AA 1.5μF capacitor is charged of 60 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Assuming that the circuit contains no resistance, the maximum current in this coil shall be close to
A1.4AB1.2AC0.8AD0.6A
A 1.5 μF capacitor is charged to 57 V. The charging battery is then disconnected , and a 12 mH coil is connected in series with the capacitor so that LC oscillations occur. What is the maximum current in the coil ? Assume that the circuit contains no resistance , which woudl cause the energy to be dissipated.
View SolutionTwo capacitors
C1=C2=1π2×10−2F and inductor L=2×10−2H are connected in series as shown in the figure. Initially charge on each capacitors are 4√3μC. At t=0 switch S1 is closed at t=1/400 sec, switch S2 is also closed. The maximum charge on capacitor C2 during LC oscillation is k√3μC. Find k

View SolutionInitially, the capacitor is charged to a potential of 5V and then connected to position 1 with the shown polarity for 1s. After 1s it is connected across the inductor at position 2
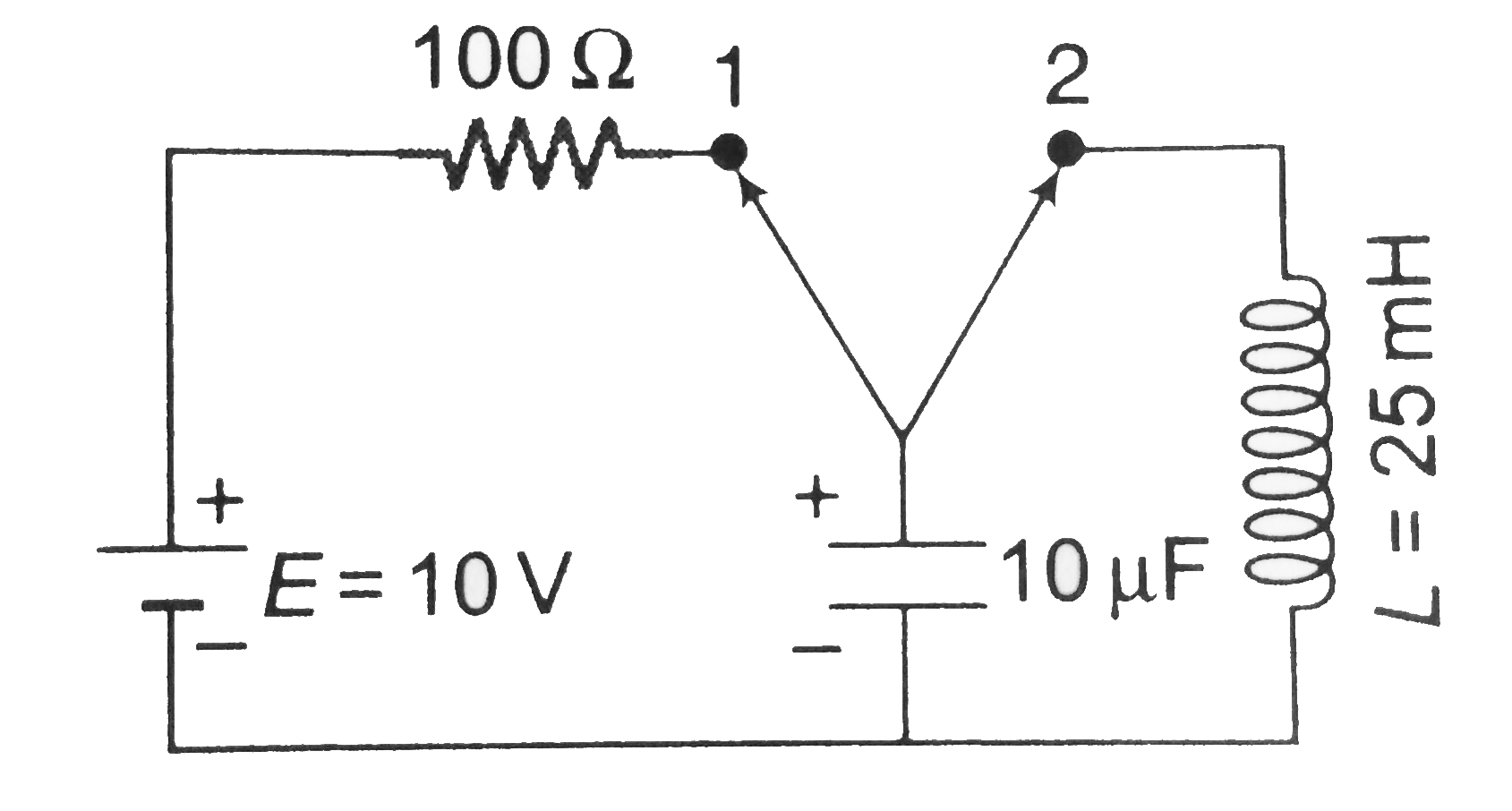
(a) Find the potential across the capacitor after 1s of its connection to position 1.
(b) Find the maximum current flowing in the L−C circuit when capacitor is connected across the inductor. Also, find the frequency of LC oscillations.
View SolutionLC Oscillator|| X-mer Question
View SolutionWhat is the mechanical equivalent of spring constant k in LC oscillating circuit?
View Solution
