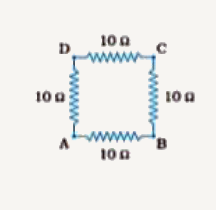
Four wires of equal length and of resistance $10 Ω$ each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is.Solution in Malayalam

$10 Ω$

$40 Ω$

$20 Ω$

$\frac{5}{2} Ω$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for Four wires of equal length and of resistance 10 Omega each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Four wires of equal length and of resistance $10 Ω$ each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is.Solution in Malayalam

The correct Answer is:A

Similar Questions

Recommended Questions

Four wires of equal length and of resistance 10Ω each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is.Solution in Malayalam

The correct Answer is:A

Similar Questions

Recommended Questions

Four wires of equal length and of resistance $10 Ω$ each are connected in the form of a square. The equivalent resistance between two opposite corners of the square is.Solution in Malayalam