Momentum of a particle is x. The corresponding wave length is
h/pv
h/x
xh
x/h
The correct Answer is:B
Similar Questions
Suppose we define a quantity Linear Momentum as linear momentum =mass x speed.
The linear momentum of a system of particles is the sum of linear momentum of the individual particles. Can we state a principle of conservation of linear momentum as linear momentum of a system remains constant if no external force acts on it?View SolutionThe momentum of a particle of wave length 1 Å is
View Solution
Knowledge Check
- Question 1 - Select One
The momentum of a proton is p. the corresponding wavelength is
Ah/pBhpCp/hD√hp - Question 2 - Select One
The momentum of a photon is p. the corresponding wavelength is
AhpBphChp2Dh√p - Question 3 - Select One
The momentum of moving particle is p . The wavelength λ of the associated matter wave will be
Ah/pBhpCp/hDp
The maximum particle velocity is 3 times the wave velocity of a progressive wave. If the amplitude of the particle is "a". The phase difference between the two particles seperated by a distance of 'x' is
View SolutionA particle of mass is confined to a narrow tube of length L.
(a) Find the wavelengths of the de-Brogile wave which will resonate in the tube.
(b) Calculate the corresponding particle moments. and
(c) Calculate the corresponding energies.View SolutionA particle of mass is confined to a narrow tube of length L.
(a) Find the wavelengths of the de-Brogile wave which will resonate in the tube.
(b) Calculate the corresponding particle moments. and
(c) Calculate the corresponding energies.View SolutionThe angular momentum of a particle is
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
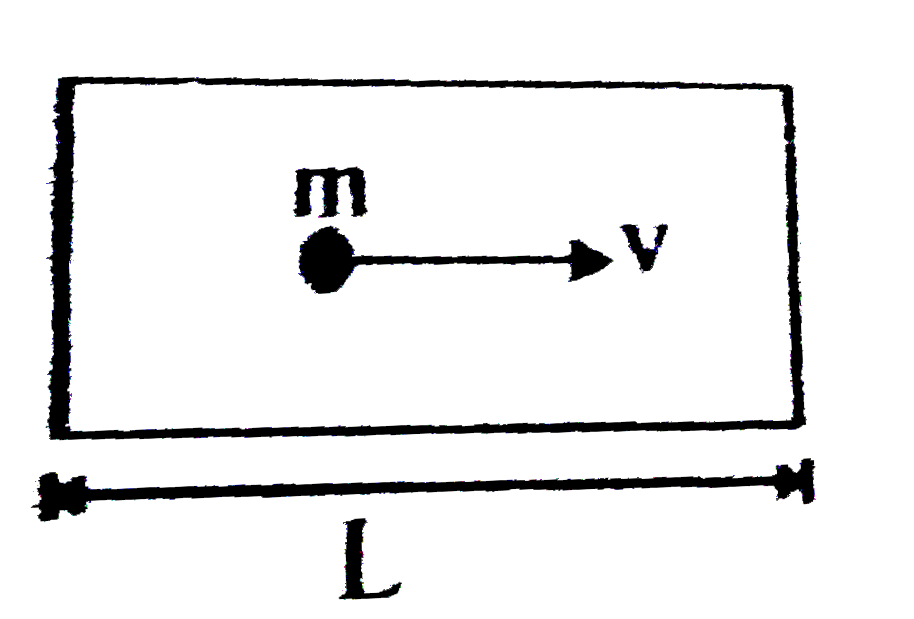
What is momentum of particle in n^(th) mode of standing wave ?View Solution

