Prove that the quadrilateral obtained by joining any two alternate vertices of a regular pentagon is cyclic.Solution in Malayalam
Step by step video & image solution for Prove that the quadrilateral obtained by joining any two alternate vertices of a regular pentagon is cyclic. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
One cubic centimetre of iron weighs 7.8 grams. Write as sequences, the volumes of weights of Iron cubes of sides 1 centimetre, 2 centimetres and so on.
View SolutionFind the following:
i) The y coordinate of any point on the 'x' axis.
ii) The 'x' coordinate of any point on the 'y' axis.
iii) The coordinates of the origin.
iv) The y coordinate of any point on the line through (0,1), parallel to the 'x' axis.
v) The x coordinate of any point on the line through (1,0), parallel to the 'y' axis.
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices ofthe quadrilateral, prove that it is a rectangle
View SolutionProve that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View SolutionProve that any four vertices of a regular pentagon are concyclic.
View Solutionसिद्ध कीजिए कि किसी चतुर्भुज के किसी भी युग्म का योगफल 180∘ हो तो चतुर्भुज चक्रीय होता है।
View SolutionProve that any four vertices of regular pentagon are concyclic .
View SolutionProve that, any rectangle is a cyclic quadrilateral.
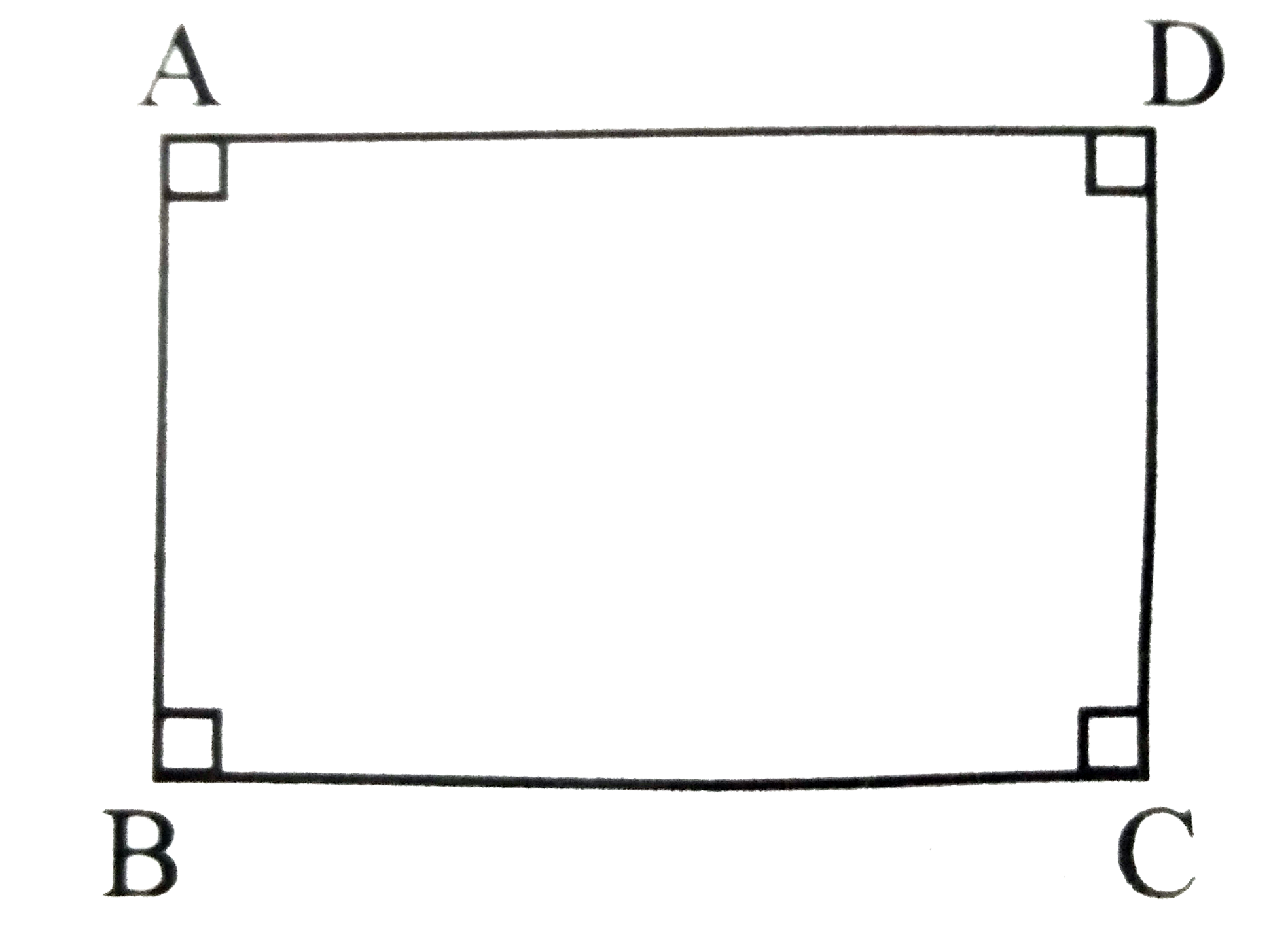
View SolutionProve that, any rectangle is a cyclic quadrilateral.
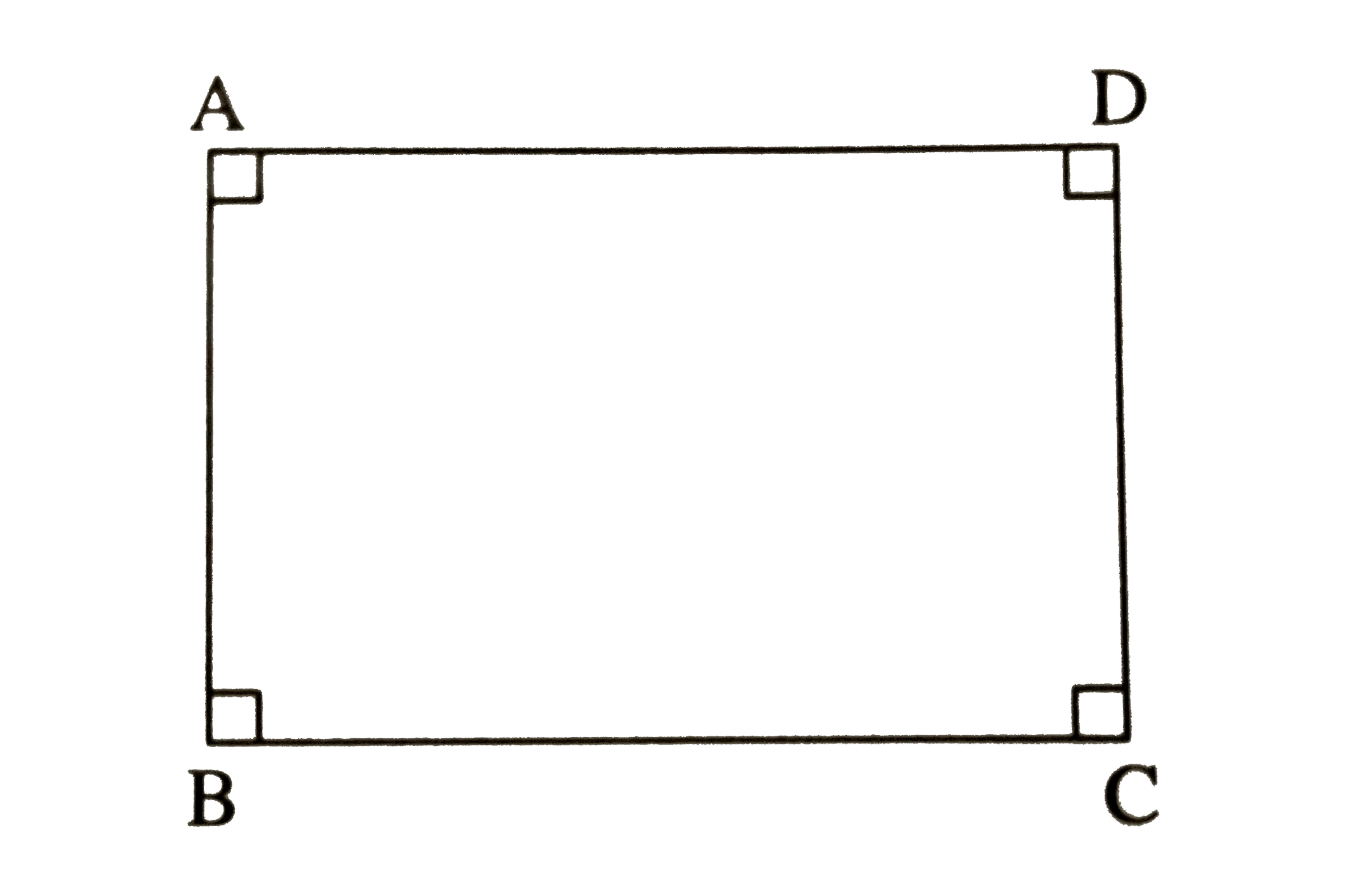
View SolutionProve that any rectangle is a cyclic quadrilateral .
Given : □PQRS is rectangle
To prove : □PQRS is cyclic quadrilateral
(##CTN_MK_MAT_X_P2_GEO_C03_E04_005_Q01.png" width="80%">
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral prove that it is a rectangle.
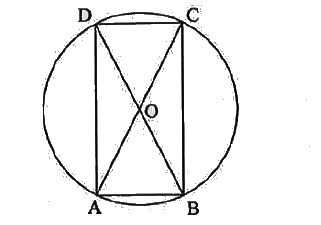
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

View SolutionIf diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
View Solution
