A tríangle got by joining alternate vertices of a regular hexagon:
'(##VPU_TTT_MAT_X_P01_C03_E03_004_Q01##)'Solution in Malayalam
Step by step video & image solution for A tríangle got by joining alternate vertices of a regular hexagon:'(##VPU_TTT_MAT_X_P01_C03_E03_004_Q01##)' by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What are the coordinates of the fourth vertex of the parallelogram shown below.
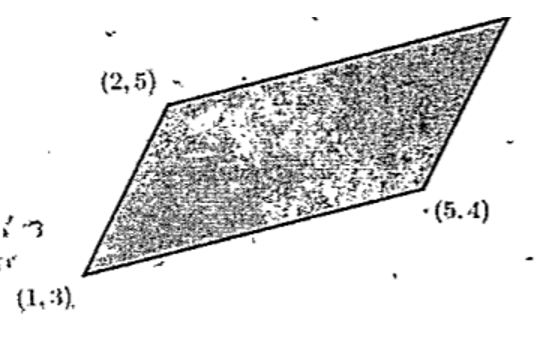
View SolutionWrite the second degree polynomials given below as the product of twofirst degree polynomials.Find also the solutions of the equation p(x)= 0 in each:- p(x)=x2−7x+12.
View SolutionThe alternate vertices of a regular hexagon are joined to form another regular hexagon. the ratio of the sides of two hexagons is
View SolutionFind the number of diagonals formed by joining the vertices of the regular hexagon.
View SolutionArea of regular polygon: regular hexagon and regular pentagon
View SolutionArea of the regular hexagon whose diagonal is the join of (2,4) and (6,7) is
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure). Find the magnitude of electric field at the centre of regular hexagon.
View SolutionA regular hexagon of side 10 cm has a charge 5μC each of its vertices, Calaculate the potential at the centre of the hexagon.
View Solutionएक षटभुज के शीर्षो को मिलाने वाले विकर्णों की संख्या ज्ञात कीजिए ।
View SolutionThe number of triangles formed by joining the vertices of a hexagon is
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
View SolutionSTARTING FROM ONE OF THE VERTICES OF A REGULAR HEXAGON , THE PARTICLE COVERS THE THREE SIDES OF THE REGULAR HEXAGON IN ORDER . WHAT IS DISPLACEMENT OF THE PARTICLE DURING THIS MOTION GIVEN THAT THE SIDE OF THIS REGULAR HEXAGON IS 'a ' units ?
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the centre of the hexagon.
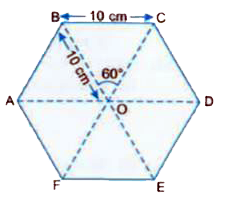
View SolutionArea of the regular hexagon whose diagonal is the join of (2,4)and(6,7) is
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure). Find the magnitude of electric field at the centre of regular hexagon.
View SolutionThe alternate vertices of a regular hexagon are joined to form another regular hexagon. The ratio of the sides of two hexagone is
View Solution
