In the figure ABCD is a square Without looking, a point marked in the figure
'(##VPU_TTT_MAT_X_P01_C03_E04_004_Q01##)'
a) Find the probability that the obmarked point lies inside the square?
b) Find the probability that the point lies in the triangle 'ABE'Solution in Malayalam
Step by step video & image solution for In the figure ABCD is a square Without looking, a point marked in the figure'(##VPU_TTT_MAT_X_P01_C03_E04_004_Q01##)' a) Find the probability that the obmarked point lies inside the square? b) Find the probability that the point lies in the triangle 'ABE' by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
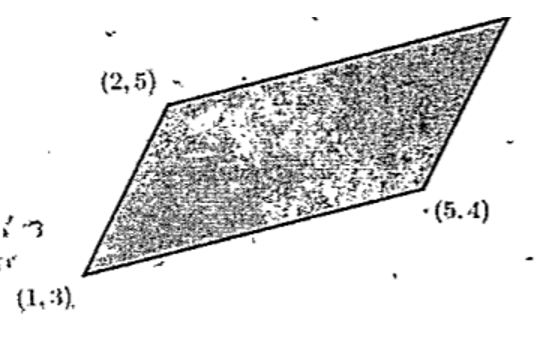
What are the coordinates of the fourth vertex of the parallelogram shown below.
View SolutionWrite the second degree polynomials given below as the product of twofirst degree polynomials.Find also the solutions of the equation p(x)= 0 in each:- p(x)=x2−7x+12.
View SolutionIn the given figure,A,B,C and D are centres of four circles that have a radius of 1 unit.If a point is selected at random from interior of square ABCD,then what is the probability that it lies in the shaded region
View SolutionIn the figure rectangle ABCD,what is the probability that a randomly chosen point that in ABCD lies inside the triangle ABE is
View SolutionA square is inscribed in a circle.If p_(r) is the probability that a randomly chosen point inside the circle lies within the square and p, is the probability that the point lies outside the square,then
View SolutionABCD एक 4 सेमी. भुजा वाला एक वर्ग है | यदि एक बिन्दु E वर्ग के अन्दर इस प्रकार स्थित है, की त्रिभुज CED एक समबाहु त्रिभुज है, तो त्रिभुज ACE का क्षेत्रफल है :
View SolutionA square is incribed in a circle . If p_(1) is the probability that a randomly chosen point of the circle lies within the square and p_(2) is the probability that the point lies outside the square then
View SolutionA point is randomly chosen inside the circumcircle of an equilateral triangle. Find the probability that it lies inside the inscribed circle of that triangle.
View SolutionA point is taken at random from inside of the circumcircle of an equilateral triangle. The probability that it lies inside the circumcircle but outside the incircle is
View SolutionIn the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionA square is inscribed in a circle with radius 7√2 units. Find the probability that a point lying inside the circle selected at random will lie inside the square.
View SolutionRead the following points. a. Cranial capacity about 900 c.c. Br b. Probably ate meat. Br c. First prehistoric man to make use of fire. These points are true for
View SolutionWite down the corresponding elements in the figure : 1)……………… br 2)…………… br 3).……………. Br 4)………….. Br 5)…………. Br 6)…………..
View SolutionIn the figure, X is a point inside the square ABCD, a square AXYZ is created above AX, then prove that BX=DZ
View SolutionA point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
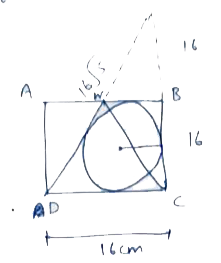
View SolutionABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
View Solution
