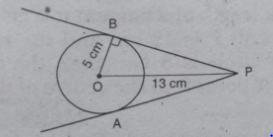
In the figure, PA, 'PB' are tarigents through 'A' and 'B' of a circle with centre 'O'.
If the radius of the cirčle is 'r', then prove. that 'O P xx O Q=r^2'.
'(##VPU_TTT_MAT_X_P02_C07_E07_004_Q01##)'Solution in Malayalam
Step by step video & image solution for In the figure, PA, 'PB' are tarigents through 'A' and 'B' of a circle with centre 'O'. If the radius of the cirčle is 'r', then prove. that 'O P xx O Q=r^2'. '(##VPU_TTT_MAT_X_P02_C07_E07_004_Q01##)' by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The distance covered by an athlete in lóng jump-practice are
'6.10,6.20,6.18,6.20,6.25,6.21,6.15,6.10'
in metres. Find the mean and median. Why is it that there is not much differerice between these?
View SolutionIn the triangle shown, what is the perpendicular distance from the top vertex to the bottom side? What is the area of the triangle?
'(##VPU_TTT_MAT_X_P01_C05_E01_001_Q01##)'
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 4.90, if PSQR , prove that POS~ROQ . (FIGURE)
View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O and radius r. If OP=2r, show that △APB is equilateral.

View SolutionFor the reaction R- Br to R- O - N =O the suitable reagent is
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionIn the figure 'O' is the centre of the circle and PA, PB are tangents , then their lenths are ……
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ.
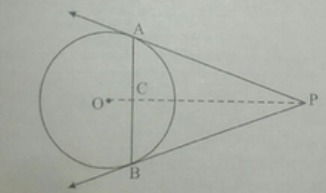
View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionIn Fig. 4.90, if POS~ROQ , prove that PSQR . (FIGURE)
View SolutionIn Fig. 4.90, if PS∣∣QR , prove that POS~ROQ . (FIGURE)
View SolutionIn Figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
View SolutionIn Fig. PQ is tangent at a point R of the circle with centre O . If ∠TRQ=30o , find ∠PRS . (FIGURE)
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
View Solution
