In Fig. PQ is tangent at a point R of the circle with centre O . If ∠TRQ=30o , find ∠PRS . (FIGURE)
To solve the problem step by step, we will use the properties of tangents and the alternate segment theorem.
1. Identify Given Information:
- We have a circle with center O.
- PQ is a tangent to the circle at point R.
- Angle TRQ = 30°.
2. Apply the Alternate Segment Theorem:
- According to the alternate segment theorem, the angle between the tangent and the chord through the point of contact is equal to the angle in the alternate segment.
- Therefore, angle TSR = angle TRQ = 30°.
3. Identify the Angle in the Semicircle:
- Since R is a point on the circle and S is another point on the circle, angle TRS is an angle subtended by the diameter (if we assume TS is a diameter).
- By the property of angles in a semicircle, angle TRS = 90°.
4. Use the Triangle Angle Sum Property:
- In triangle SRT, the sum of angles is 180°.
- We have angle RTS + angle TRS + angle RST = 180°.
- We know angle TRS = 90° and angle TSR = 30°.
- Therefore, angle RTS = 180° - (90° + 30°) = 60°.
5. Conclude with the Required Angle:
- By the alternate segment theorem, angle PRS = angle RTS.
- Thus, angle PRS = 60°.
Final Answer:
Angle PRS = 60°.
---
- We have a circle with center O.
- PQ is a tangent to the circle at point R.
- Angle TRQ = 30°.
- According to the alternate segment theorem, the angle between the tangent and the chord through the point of contact is equal to the angle in the alternate segment.
- Therefore, angle TSR = angle TRQ = 30°.
- Since R is a point on the circle and S is another point on the circle, angle TRS is an angle subtended by the diameter (if we assume TS is a diameter).
- By the property of angles in a semicircle, angle TRS = 90°.
- In triangle SRT, the sum of angles is 180°.
- We have angle RTS + angle TRS + angle RST = 180°.
- We know angle TRS = 90° and angle TSR = 30°.
- Therefore, angle RTS = 180° - (90° + 30°) = 60°.
- By the alternate segment theorem, angle PRS = angle RTS.
- Thus, angle PRS = 60°.
Angle PRS = 60°.
Topper's Solved these Questions
Similar Questions
In Fig. 10.96, if TP and TQ are tangents drawn from an external points T to a circle with centre O such that ∠TQP=60o , then ∠OPQ= (FIGURE) 25o (b) 30o (c) 40o (d) 60o
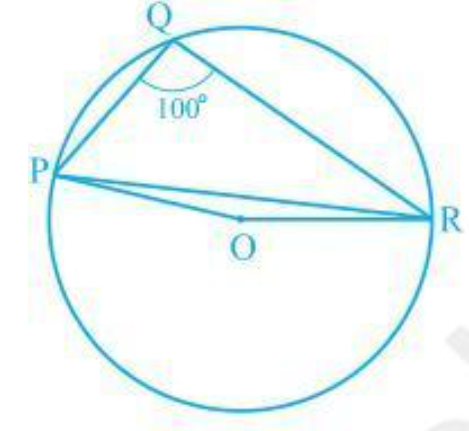
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (a) 67o (b) 134o (c) 44o (d) 46o
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View SolutionIn Figure, O is the centre of a circle and PQ is a diameter. If ∠ROS=400, find ∠RTS
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View SolutionIn Figure, ∠PQR=1000, where P, Q and R are points on a circle with centre. O. Find ∠OPR
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn Fig. 10.76, CP and CQ are tangents from an external point C to a circle with centre O . AB is another tangent which touches the circle at R . If CP=11cm and BR=4cm , find the length of BC . (FIGURE)
View SolutionIn Fig. 10.74, CP and CQ are tangents to a circle with centre O . ARB is another tangent touching the circle at R . If CP=11cm and BC=7cm , then find the length of BR . (FIGURE)
View Solution
