In the picture below, the yellow rectangle is drawn. joining one vertex of the green ∴ square and the mid-points of its two sides:
What tion of the area of the square is, the area of the triangle?
'(##VPU_TTT_MAT_VI_P02_C11_E03_002_Q01##)'
38 of the area of the square ts the area of the triangle.
Topper's Solved these Questions
Similar Questions
Let P, Q, R be the mid-points of sides AB, BC, CA respectively of a triangle ABC. If the area of the triangle ABC is 5 square units, then the area of the triangle PQR is
View SolutionOut of a square of side 8 cm, a triangle is drawn with base as one side of the square and third vertex at any point on the opposite side of the square. What is the area of the remaining portion of the square if the triangle is taken out? (a) 16 sq. cm (b) 32 sq. cm (c) 64 sq. cm (d) Cannot be determined (e) None of these
View Solution
Knowledge Check
Two goats tethered to diagonally opposite vertices of a field formed by joining the mid-points of the adjacent sides of another square field of side 20√2 . What is the total grazing area of the two goats?
A100πm2B50(√2−1)πm2C100π(3−2√2)m2D200π(2−√2)m2In the figure shown square II is formed by joining the mid-points of square II
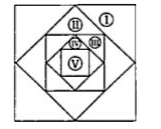
and so on . In this way total five squares are drawn . The sides of the square I is 'a' cm.
What is the total area of all the five squares ?A(4√2−1)a2(4√2−1)B(4√2−1)a24(√2−1)C3116a3Dnone of theseABCD is a square . A circle is inscribed in the square . Also taking A,B,C,D ( the vertices of squares ) as the centres of four quadrants , drawn inside the circel , which are touching each other on the mid-points of the sides of square . Area of square is 4cm2. What is the area of the shaded region ?
 A(4−3π2)cm2B(2π−4)cm2C(4−2π)cm2Dnone of these
A(4−3π2)cm2B(2π−4)cm2C(4−2π)cm2Dnone of these
Suppose P, Q and R are the mid-points of sides of a triangle of area 128cm2. If a triangle ABC is drawn by joining the mid-points of sides of triangle PQR, then what is the area of triangle ABC?
View SolutionSquare of the area of the triangle formed by end points of a focal chord PQ of length 32 units of the parabola y2=8x and its vertex is
View SolutionA square is drawn by joining the mid-points of the sides of a square. A third square is drawn inside the second square in the same way and the processes continued indefinitely. If the side of the square is 10cm , find the sum of the areas of all the squares so formed.
View SolutionThe area of a triangle is 32 square units. Two of its vertices are the points A(2,−3) and B(3,−2), the third vertex of the triangle lies on the line 3x−y−2=0, then third vertex C is
View SolutionA square is drawn by joining mid-points of the sides of a square. Another square is drawn inside the second square in the same way and the process is continued indefinitely. If the side of the first square is 16 cm, then what is the sum of the areas of all the squares ?
(a)256sq. Cm
(b)512 sq. cm
(c)1024sq. Cm
(d)512/3sq. Cm
View Solution
