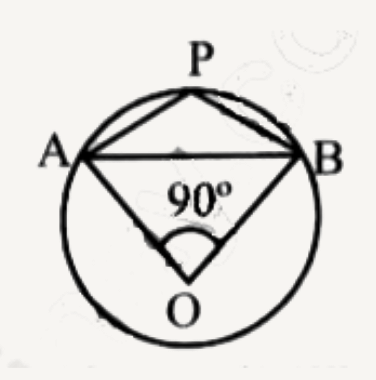
In the figure, O is the centre and' AB=BC.
(a) Prove that ∠AOB=∠BOC.
(b) If OA=AB=BC, then find ∠AOB,∠BOC.
Text Solution
In ΔAOB⋅ and ΔBOC, AB=BC,AO=CO,BO=BO Since the sides of ΔAOB are equal to the sides of ΔBOC, angles opposite fo the equal sides are equal. Therefore, ∠AOB=∠BOC If OA=AB=BC, then,ΔAOB and ΔBOC are equilateral triagles. ∠AOB=∠BOC=60∘
|
Similar Questions
Knowledge Check
In the given figure, find ∠AOB.
 A140∘B120∘C150∘D160∘
A140∘B120∘C150∘D160∘In triangle ABC, O is the orthocenter and angle BOC is 120∘. Calculate angle BAC.
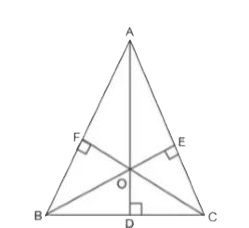 A30∘B40∘C60∘D80∘
A30∘B40∘C60∘D80∘
In the given AB=BC=DCand∠AOB=50∘
∠BOD
View SolutionIn the given figure, find ∠AOB.

View SolutionO is the incentre of ΔABC and ∠A=30∘, then find ∠BOC.
View SolutionIn the given AB=BC=DCand∠AOB=50∘
∠AOD
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View Solution