A block of mass m is pulled on an incline surface having coefficient of friction μ=1& angle of inclination θ=30∘, with the horizontal, such that required external force is minimum. The angle made by this force with the incline is :
45∘
30∘
75∘
53∘
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the block on the incline and determine the angle made by the external force with the incline when the required external force is minimized.
Step 1: Identify the forces acting on the block
- The weight of the block W=mg acts vertically downward.
- The normal force N acts perpendicular to the incline.
- The frictional force f acts parallel to the incline, opposing the motion.
- An external force F is applied at an angle α with the incline.
Step 2: Resolve the forces
- The weight can be resolved into two components:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
- The external force F can also be resolved:
- Parallel to the incline: F∥=Fcosα
- Perpendicular to the incline: F_{\perpendicular} = F \sin \alpha
Step 3: Write the equations of motion
Using the equilibrium conditions along the incline and perpendicular to the incline:
1. Along the incline:
Fcosα−f−mgsinθ=0
The frictional force f can be expressed as f=μN.
2. Perpendicular to the incline:
N+Fsinα−mgcosθ=0
Step 4: Express the normal force
From the second equation, we can express the normal force N:
N=mgcosθ−Fsinα
Step 5: Substitute N in the first equation
Substituting N into the first equation gives:
Fcosα−μ(mgcosθ−Fsinα)−mgsinθ=0
Step 6: Rearranging the equation
Rearranging the equation leads to:
Fcosα+μFsinα=mgsinθ+μmgcosθ
Step 7: Factor out F
Factoring out F:
F(cosα+μsinα)=mg(sinθ+μcosθ)
Step 8: Find the minimum force condition
To minimize F, we need to maximize the term cosα+μsinα. This occurs when:
tanα=μ
Thus, the angle α can be calculated as:
α=tan−1(μ)
Step 9: Substitute the value of μ
Given μ=1:
α=tan−1(1)=45∘
Conclusion
The angle made by the external force with the incline when the required external force is minimized is:
α=45∘
- The weight of the block W=mg acts vertically downward.
- The normal force N acts perpendicular to the incline.
- The frictional force f acts parallel to the incline, opposing the motion.
- An external force F is applied at an angle α with the incline.
- The weight can be resolved into two components:
- Parallel to the incline: W∥=mgsinθ
- Perpendicular to the incline: W_{\perpendicular} = mg \cos \theta
- Parallel to the incline: F∥=Fcosα
- Perpendicular to the incline: F_{\perpendicular} = F \sin \alpha
Using the equilibrium conditions along the incline and perpendicular to the incline:
Fcosα−f−mgsinθ=0
The frictional force f can be expressed as f=μN.
N+Fsinα−mgcosθ=0
From the second equation, we can express the normal force N:
N=mgcosθ−Fsinα
Substituting N into the first equation gives:
Fcosα−μ(mgcosθ−Fsinα)−mgsinθ=0
Rearranging the equation leads to:
Fcosα+μFsinα=mgsinθ+μmgcosθ
Factoring out F:
F(cosα+μsinα)=mg(sinθ+μcosθ)
To minimize F, we need to maximize the term cosα+μsinα. This occurs when:
tanα=μ
Thus, the angle α can be calculated as:
α=tan−1(μ)
Given μ=1:
α=tan−1(1)=45∘
The angle made by the external force with the incline when the required external force is minimized is:
α=45∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :
 View Solution
View SolutionA mass placed on an inclined place is just in equilibrium. If μ is coefficient of friction of the surface, then maximum inclination of the plane with the horizontal is
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
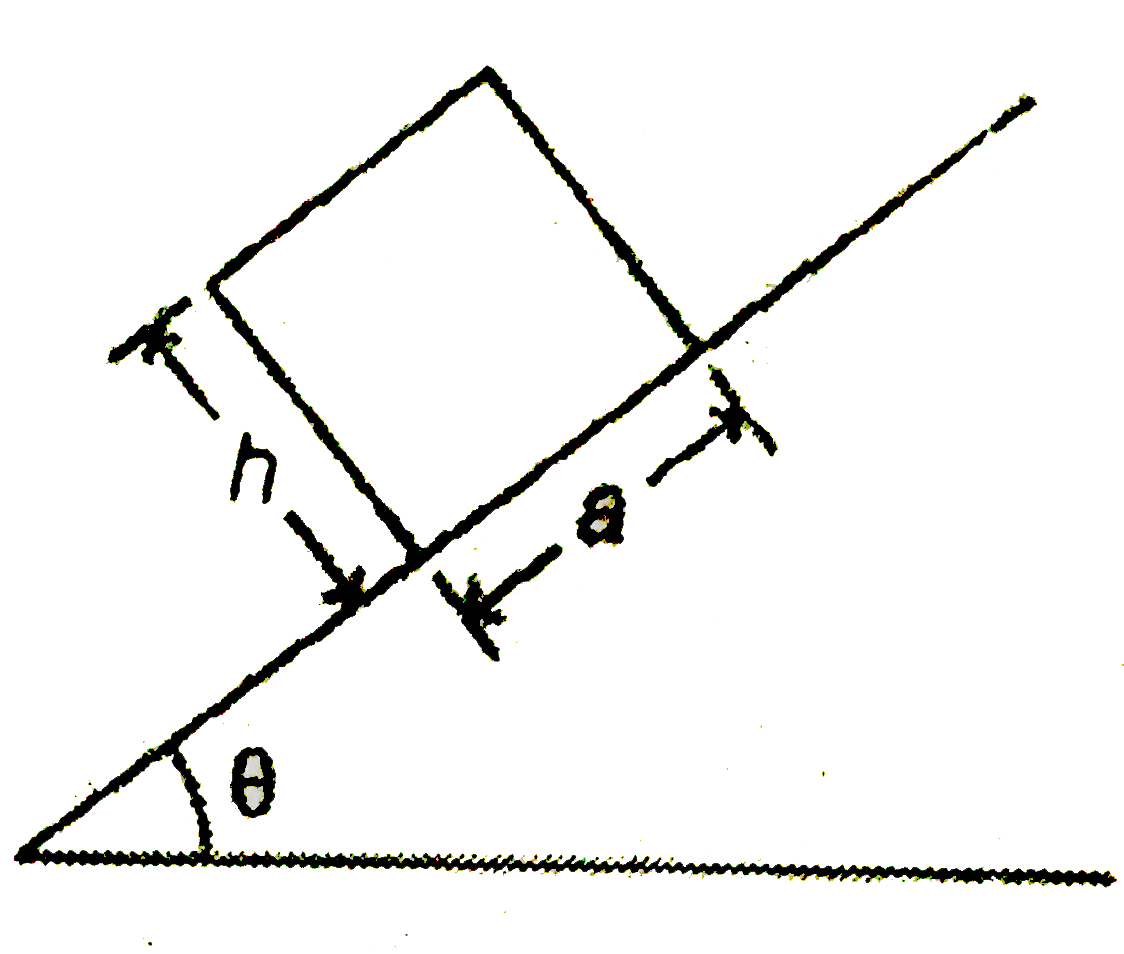 View Solution
View Solution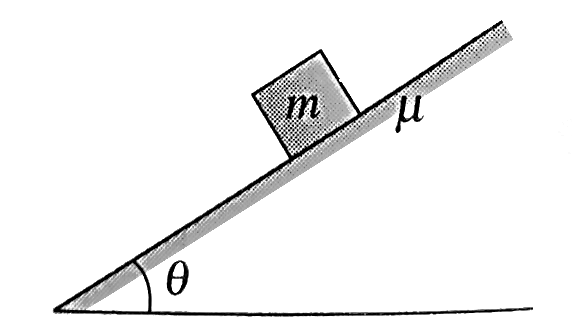 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If μ=34 then what will be frictional force (shear force) acting between the block and inclined plane when θ=30∘:View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution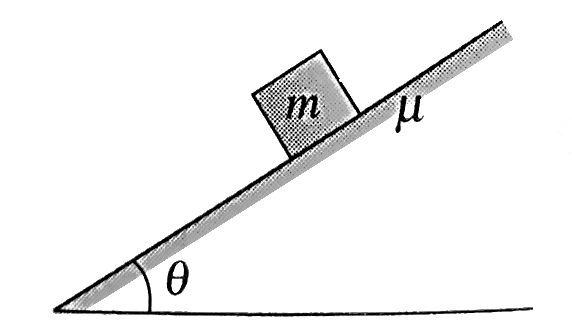 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:View Solution

