One has to throw a particle from one side of a fixed sphere, in a diameterical plane to another side such that it just grazes the sphere. Minimum possible speed for this is √2gR(√α+√β). Find α+β
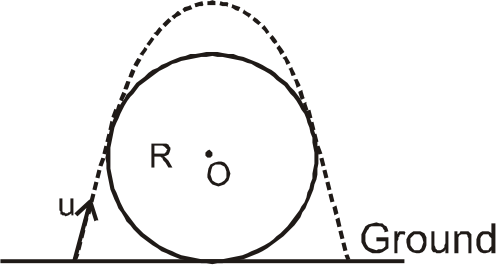
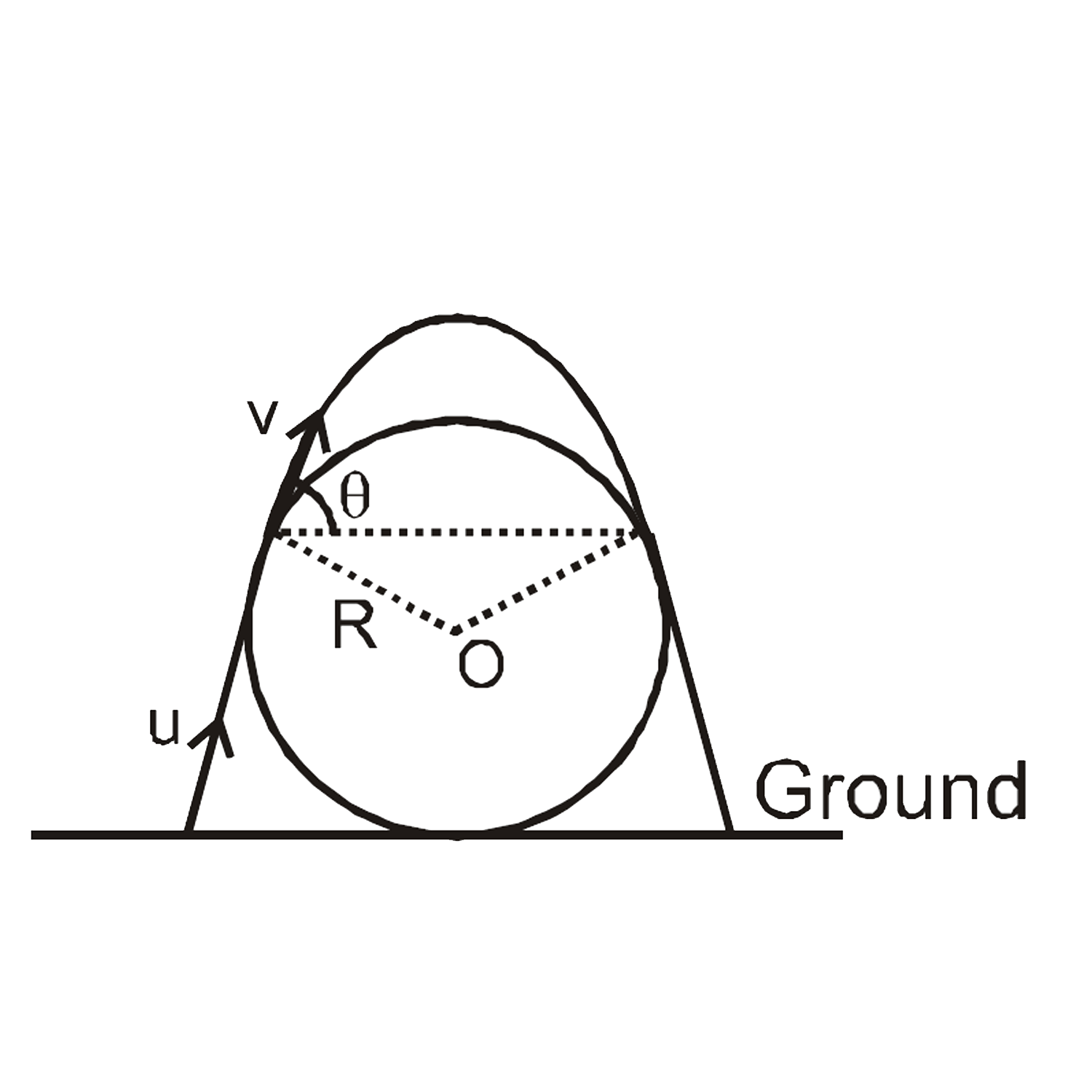
2V2sinθcosθg=2Rsinθ⇒v2=Rgcosθ
u2=V2+2gR(1+cosθ)
u2=Rgcosθ+2gR+2gRcosθ
u2=Rg(1+2cos2g)cosθ+2gR
for u to be minimum 1+2cos2θcosθ=min
⇒cosθ=1√2⇒θ=π/4
umin=√√2Rg+2gR+√2Rg=√2gR(√2+1)
Topper's Solved these Questions
Similar Questions
Evaluate: ∫dx√sin(x+α)cos3(x−β)
View SolutionAray of light falls on one side of a prism whose refracting angle is 75∘. Find the angle of incidence in order that the emergent ray may just graze the other side, (μ=√2)
View SolutionA particle performs simple harmonic motion with amplitude A. its speed is double at the instant when it is at distance A3 from equilibrium position. The new amplitude of the motion is √33Aβ. Find β
View SolutionIf a chord which is normal to the parabola at one end subtend a right angle at the vertex, then angle to the axis is (a) α=√2 (b) α=√3 (c) α=1√2 (d) α=1√3
View SolutionIf the quadratic equation x2−36x+λ=0 has roots α and β such that α, β∈N and (lambda)/(5) cancel in Z and λ assumes minimum possible value then √α+2√β+2|α−β| is equal to (a) 38 (b) 316 (c) √11134 (d) √11117
View SolutionEvaluate ∫dx(√(x−α)2−β2)(ax+b).
View SolutionIf (α,β) is a point of intersection of the lines xcosθ+ysinθ=3 and xsinθ−ycosθ=4 where θ is parameter, then maximum value of 2α+β√2 is
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionProblem on sine rule Type:-2 (i)The angle of elevation of the top of the tower from a point A due South of the tower is α and from B due east of the tower is β. If AB=d Show that the height of the tower is d√cot2α+cot2β (ii) A tree stands vertically on a hill side which makes an angle of 15∘ with the horizontal. From a point on the ground 35m down the hill from the base of the tree ; the angle of elevation of the top of the tree is 60∘ .find the height of the tree ?
View SolutionIf 4sin27∘=√α−√β, then the value of (α+β−αβ+2)4 must be
View Solution

