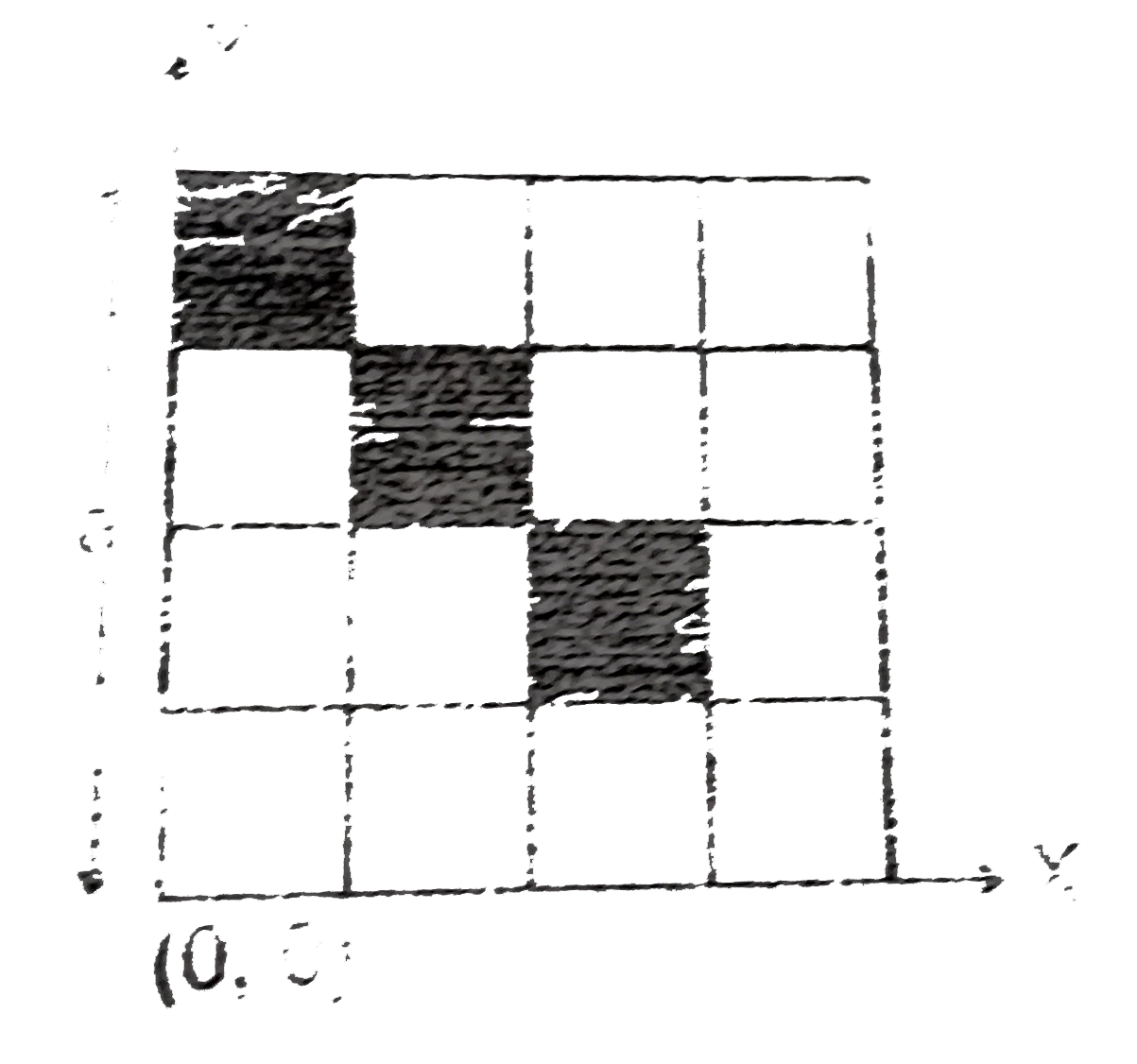
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
−π(π−2)l2(8−π)
π(π−2)l2(8−π)
−π(π−2)l8−π
−l(π−43)2(8−π)
xcm=m1x1+m2x2m1+m2
m1=mass of square plate
=m
x1=c.m. of square plate =0
m2 =mass of removed part
=−ml2⎛⎜⎝πl242⎞⎟⎠=−π8m
x2=c.m. of removed part
=l2−43π(l2)=l2(1−43π)
∴xcm=−πm8.l2(1−43π)m−π8m,xcm=−l(π−43)2(8−π)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The x, y coordinates of the centre of mass of a uniform L-shaped lamina of mass 3 kg is
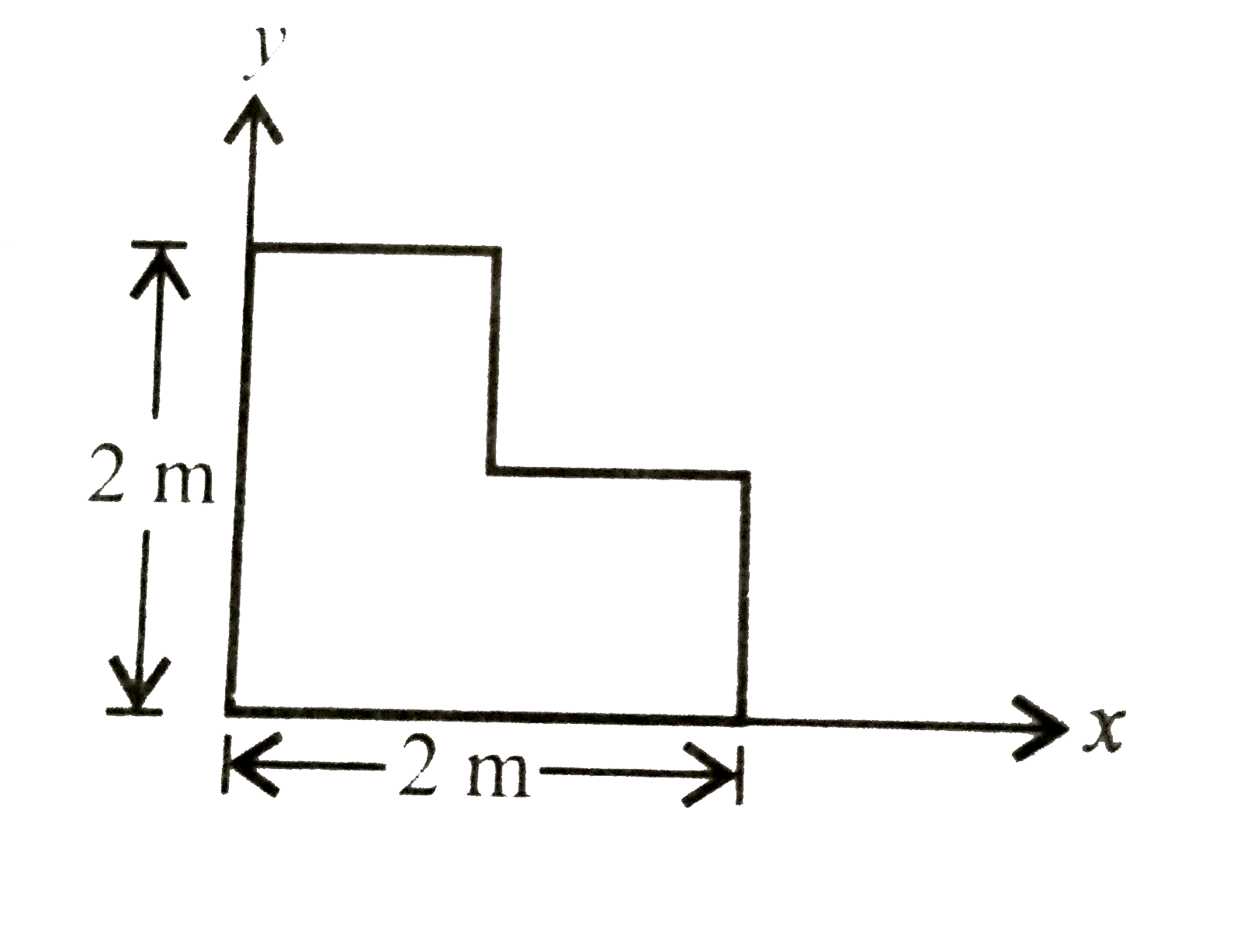 A(5/6 m, 5/6 m)B(1 m, 1 m)C(6/5 m, 6/5 m)D(2 m, 2m)
A(5/6 m, 5/6 m)B(1 m, 1 m)C(6/5 m, 6/5 m)D(2 m, 2m)

From a uniform square plate of side a and mass m, a square portion DEFG of side a2 is removed. Then, the moment of inertia of remaining portion about the axis AB is
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.

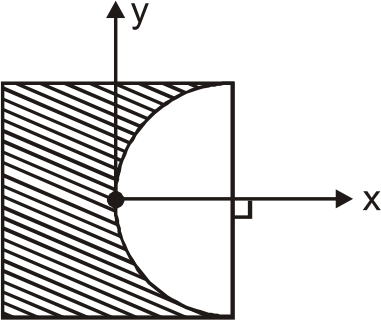
View SolutionAs shown in figure, when a semicircular cavity is cut from a square plate. Position of com is at
View SolutionAs shown in figure, when a semicircular cavity is cut from a square plate. Position of com is at

View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
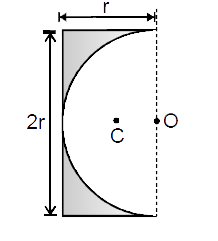
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
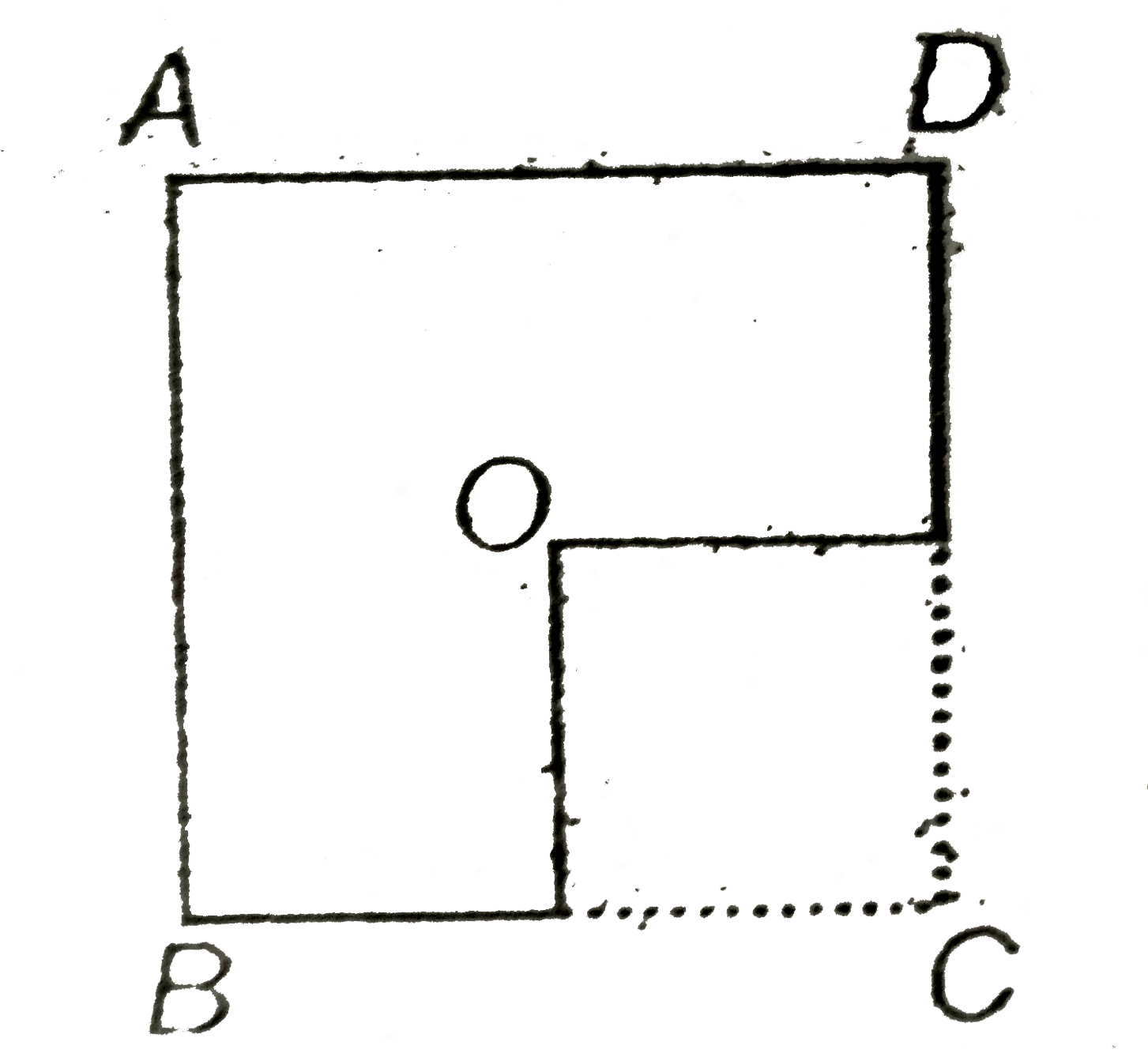
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on

View Solution