Power of the only force acting on a particle of mass m = 1 kg moving in a straight line depends on its velocity as P=v2 where v is in ms−1 and P is in watt. If the initial velocity of the particle is 1ms−1, then the displacement of the particle in ln(2) seconds will be
(ln2−1)m
(ln2)2m
1m
2m
P=Fv
v2=Fv
Ma=v
1×vdvdx=v
∫v1dv=∫x0dx
v-1=x
v=x+1
dxdt=x+1
∫x0dxx+1=∫t0dt
ln(x+1)−ln(0+1)=t
x+1=et
x=et−1
at t=ln2
x=2−1=1m
Topper's Solved these Questions
Similar Questions
Power of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionA particle moving in a straight line has velocity-displacement equation as v=5√1+s. Here v is in ms−1 and s in metres. Select the correct alternative.
View SolutionA particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
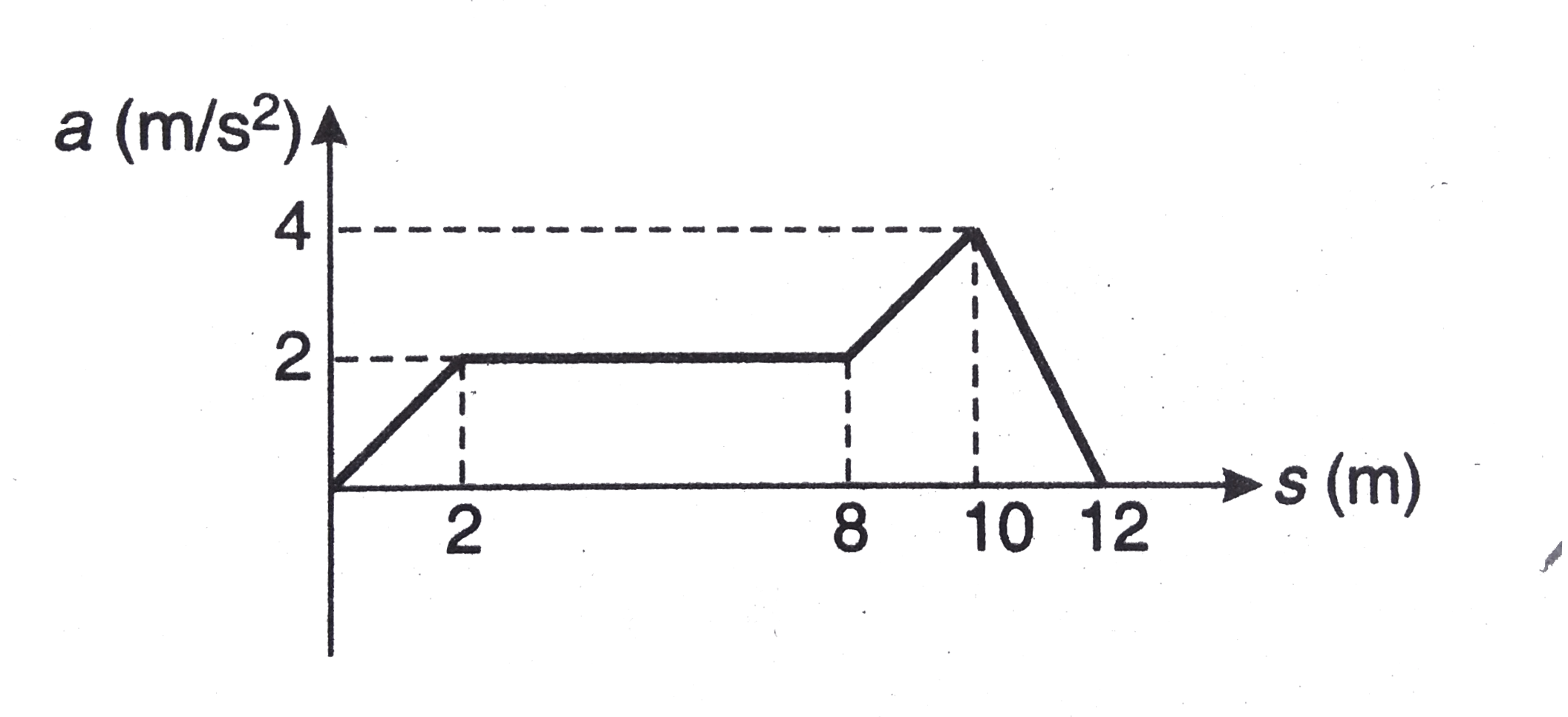
View SolutionA particle of mass 2kg travels along a straight line with velocity v=a√x, where a is a constant. The work done by net force during the displacement of particle from x=0 to x=4m is
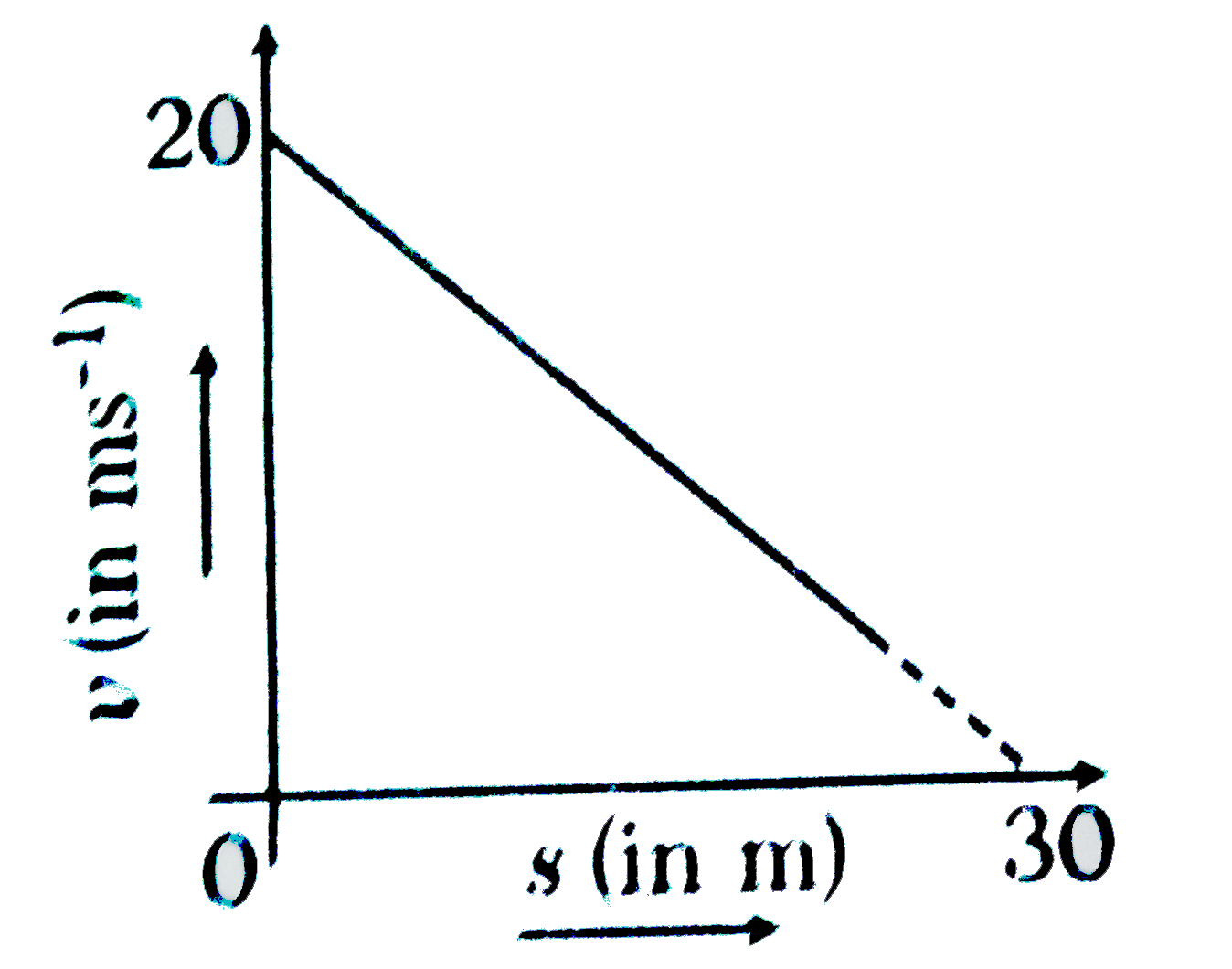
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View SolutionEquation of motion of a body is dvdt=−4v+8, where v is the velocity in ms−1 and t is the time in second. Initial velocity of the particle was zero. Then,
View Solution
