Consider a parabola y=Ax2+B,−x0≤x≤x0.
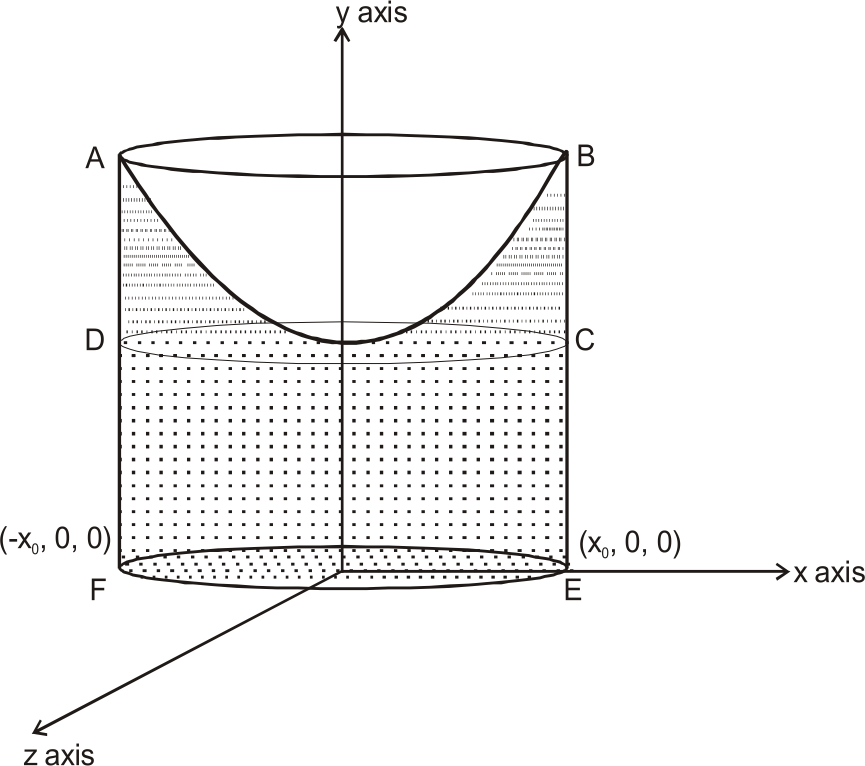
If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by V=πAx402+πBx20=volume of cylinder ABCD2+Volume of cylinder CDEF
Use the above result to answer following question.
If the cylinder of previous problem was completely filled, then the minimum angular velocity at which base may be visible is.
√gha2
√2gha2
√gh2a2
√43gha2
y=ω2x22g
h=ω2a22g
ω=√2gha2
Topper's Solved these Questions
Similar Questions
Consider a parabola y=Ax2+B,−x0≤x≤x0.
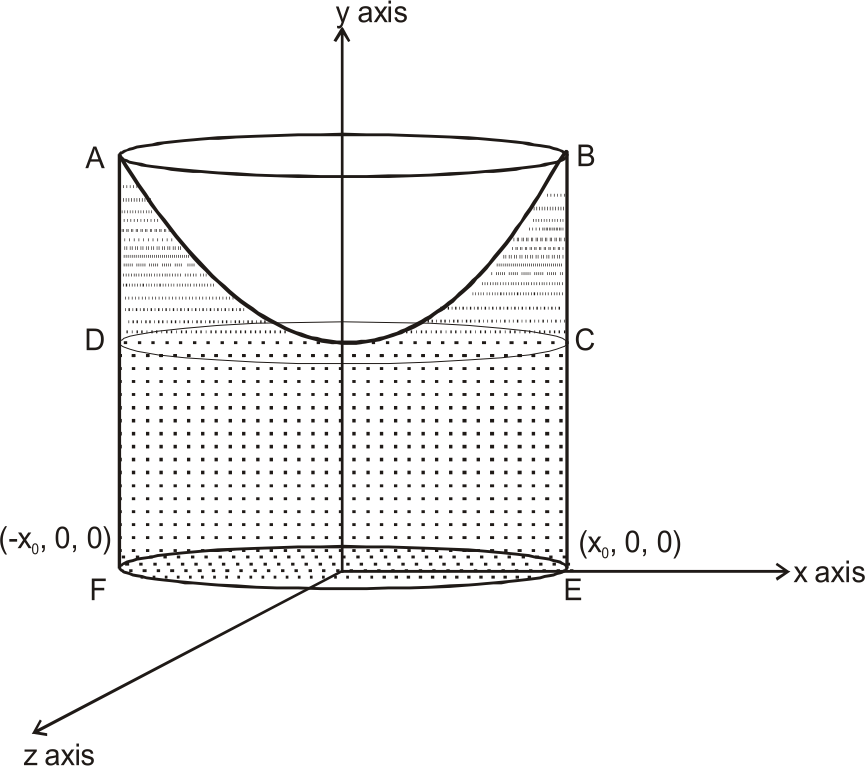
If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by V=πAx402+πBx20=volume of cylinder ABCD2+Volume of cylinder CDEF
Use the above result to answer following question.
A cyllindrical container of height ‘h’ and radius ‘a’ is two-third filled. Find maximum angular velocity at which liquid can be rotated without spilling it.View SolutionConsider a parabola y=Ax2+B,−x0≤x≤x0.
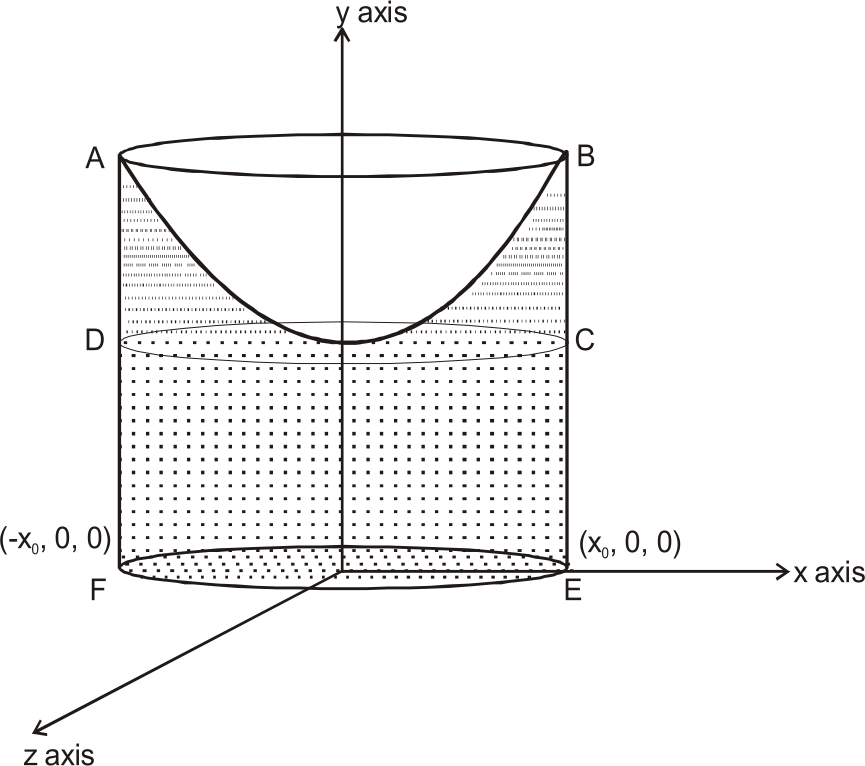
If this curve is rotated about y axis, we get a paraboloid surface. The volume below this surface & above x–z plane is given by V=πAx402+πBx20=volume of cylinder ABCD2+Volume of cylinder CDEF
Use the above result to answer following question.
In the above situation (i.e. fully filled cylinder of radius ‘a’ and height ‘h’), if liquid is rotated at twice the angular velocity found in previous problem, then the amount of liquid left (after spillage) in the cylinder will be :View Solution
Knowledge Check
- Question 1 - Select One
If the region bounded by the lines y=−43x+4 , x=0 , and y=0 is rotated about the y-axis, the volume of the figure formed is
A18.8B37.7C56.5D84.8 - Question 2 - Select One
The region in the first quadrant bounded by the line 3x+2y=7 and the coordinate axes is rotated about the x-axis .What is the volume of the resulting solid ?
A8 units3B20 units3C30 units3D40 units3
Area between the x-axis and the curve y=cosx, when 0≤x≤2π is:
View Solutionx−y≤2,x+y≤4,x≥0,y≥0
View Solutiony−2x≤1,x+y≤2,x≥0,y≥0
View SolutionA solid cylinder of mass 20kg rotates about its axis with angular velocity of 100 radian s−1. The radius of the cylinder is 0.25m. The magnitude of the angular momentum of the cylinder about its axis of rotation is
View SolutionA solid cylinder has a total surface area of 231 cm2. Its curved surface area is 23 of the total surface area. Find the volume of the cylinder.
View SolutionA solid cylinder has a total surface area of 231 cm2. Its curved surface area is 23 of the total surface area. Find the volume of the cylinder.
View Solution

