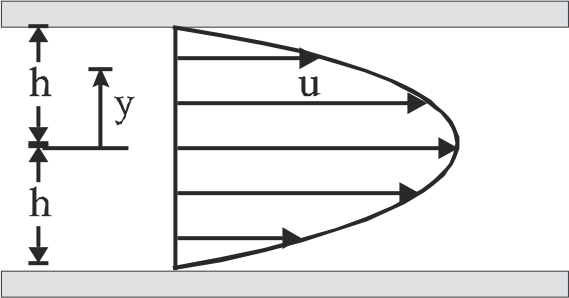
The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
![The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation u=(3V)/2[1-(y/h)^(2)] where V is the mean velocity. The fluid has coefficient of viscosity eta Answer the following 3 questions for this situation. Shear stress acting on the bottom wall is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_07_E01_040_Q01.png)
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall is
τbottom wall=η(3Vh)
τbottom wall=η(3V2h)
τbottom wall=η(6Vh)
τbottom wall=η(Vh)
For this type of parallel flow the shearing stress is given as ta=ηdudy....(i)
For the given distribution
dudy=−3Vyh2....(ii)
(a) Along the bottom wall so that (from eq. (ii))
dudy=3Vh and therefore the shearing stress is τbottom wall=η(3Vh)
(b) Along the plane where y=h/2 it follows from equation (ii) that
dudy=−3Vyh2 and thus the shearing stress is |τ|=η3V2h.
(C) 
Rate of volume flow
2∫h03V2(1−y2h2)dy.l=2Vlh
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased, then
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation u=(3V)/2[1-(y/h)^(2)] where V is the mean velocity. The fluid has coefficient of viscosity eta Answer the following 3 questions for this situation. Shear stress acting on the bottom wall is
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation

u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is
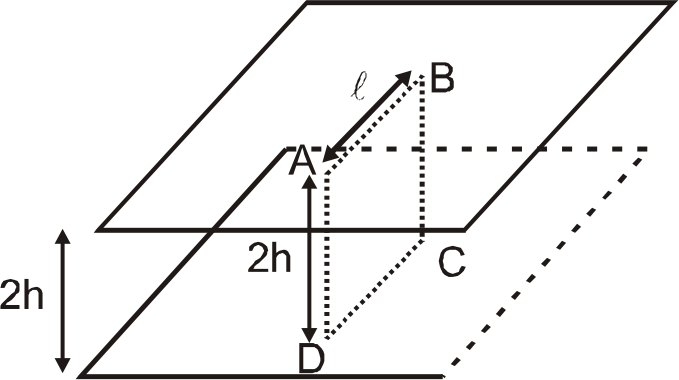
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
View SolutionA tube of length 1 and radius R carries a steady flow of fluid whose density is ρ and viscosity η. The velocity v of flow is given by v=v0(1−r2/R2) Where r is the distance of flowing fluid from the axis.
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha(d' theta)/(dt) but y(d' theta)/(dt)=u,(d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. In previous question the value of constant speed of palte (m//sec.) is equal to
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. If velocity distribution is given as (parabolic) u = c_(1)y^(2) + c_(2)y + c_(3) For the same force of 2N and the speed of the plate 2 m//sec , the constant C_(1), C_(2) & C_(3) are
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just below the plate, in above problem is equal to - (per second)
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force. In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation - (F)/(A) alpha (d' theta)/(dt) but y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y) then F = eta A(u)/(y), eta = coefficient of viscosity for non-linear velocity distribution - F = eta A(du)/(dy) where (u)/(y) or (du)/(dy) is known as velocity gradiant. The velocity gradient just near the bottom boundary is equal to -
View SolutionShow that Reynold's number R=ρv0dη is dimensionless. (ρ is density of the fluid, v0 is the critical velocity, d is diameter through which the fluid is flowing and η is the coefficient of viscosity of the fluid).
View SolutionShow that Reynold.s number R=(rhov_(0)d)/(eta) is dimensitons ( rho is density fo the fluid, v_(0) is the critical velocity, d is diameter through which the fluid is flowing and eta is the coefficient of viscosity of the fluid).
View SolutionThe velocity of water in river is 180 km h^(-1) near the surface .If the river is 5 m deep,then the shearing stress between the surface layer and the bottom layer is ( coefficient of viscosity of water eta =10^(-3) Pa s)
View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation

u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is

View SolutionThe velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation u=(3V)/2[1-(y/h)^(2)] where V is the mean velocity. The fluid has coefficient of viscosity eta Answer the following 3 questions for this situation.
View Solution
