Match the statements given in column-I with their corresponding possible results in column-II.
Column-IColumn-II(P) If photons of ultraviolet light of energy 12 eV are incident on a metal surface of work function of 4 eV, then the stopping potential (in eV) will be (1)8(Q)The ratio of wavelengths of Kα lines of two elements is (8581)2 Number of elements having atomic number between these elements will be (2)3(R) If 20 gm of a radioactive substance due to radioactive decay reduces to 10 gm in 4 minutes, then in what time (in minutes) 80 gm of the same substance will reduce to 20 gm(3)8(S)The mass defect for the nucleus of helium is 0.0302a.m.u. The binding energy per nucleon for helium in MeV is approximately(1amu=930MeV/c2)(4)7
PQRS(A)2134
PQRS(B)1214
PQRS(C)2431
PQRS(D)1243
To solve the problem, we will match the statements in Column-I with their corresponding results in Column-II step by step.
Step 1: Analyzing Statement P
Statement P: If photons of ultraviolet light of energy 12 eV are incident on a metal surface with a work function of 4 eV, then the stopping potential (in eV) will be.
- Given:
- Energy of photons (E) = 12 eV
- Work function (φ) = 4 eV
- Stopping potential (V₀) can be calculated using the formula:
V₀ = \frac{E - φ}{e}
where e is the charge of an electron (which cancels out in eV).
- Calculation:
V₀=12 eV−4 eV=8 eV
Conclusion for P:
- Match: P → (1) 8
---
Step 2: Analyzing Statement Q
Statement Q: The ratio of wavelengths of "K_alpha" lines of two elements is (8581)2. The number of elements having atomic numbers between these elements will be.
- Given:
- Ratio of wavelengths: (8581)2
- Using the formula for the ratio of wavelengths:
z1−1z2−1=8581
- Let’s assume:
- z1=86 and z2=82 (solving gives these atomic numbers).
- Counting elements between atomic numbers 82 and 86:
- Elements: 83, 84, 85 (total = 3).
Conclusion for Q:
- Match: Q → (2) 3
---
Step 3: Analyzing Statement R
Statement R: If 20 gm of a radioactive substance reduces to 10 gm in 4 minutes, then in what time (in minutes) will 80 gm of the same substance reduce to 20 gm?
- Given:
- Initial mass = 20 gm → Final mass = 10 gm in 4 minutes.
- This indicates a half-life of 4 minutes.
- To find the time for 80 gm to reduce to 20 gm:
- 80 gm → 40 gm (4 minutes)
- 40 gm → 20 gm (4 minutes)
- Total time:
4 minutes+4 minutes=8 minutes
Conclusion for R:
- Match: R → (3) 8
---
Step 4: Analyzing Statement S
Statement S: The mass defect for the nucleus of helium is 0.0302 a.m.u. The binding energy per nucleon for helium in MeV is approximately.
- Given:
- Mass defect (Δm) = 0.0302 a.m.u.
- 1 a.m.u. = 930 MeV/c².
- Binding energy per nucleon:
Binding Energy=Δm×930 MeVA
where A (mass number of helium) = 4.
- Calculation:
Binding Energy per nucleon=0.0302×9304≈7 MeV
Conclusion for S:
- Match: S → (4) 7
---
Final Matching:
- P → (1) 8
- Q → (2) 3
- R → (3) 8
- S → (4) 7
Statement P: If photons of ultraviolet light of energy 12 eV are incident on a metal surface with a work function of 4 eV, then the stopping potential (in eV) will be.
- Energy of photons (E) = 12 eV
- Work function (φ) = 4 eV
V₀ = \frac{E - φ}{e}
where e is the charge of an electron (which cancels out in eV).
V₀=12 eV−4 eV=8 eV
- Match: P → (1) 8
Statement Q: The ratio of wavelengths of "K_alpha" lines of two elements is (8581)2. The number of elements having atomic numbers between these elements will be.
- Ratio of wavelengths: (8581)2
z1−1z2−1=8581
- z1=86 and z2=82 (solving gives these atomic numbers).
- Elements: 83, 84, 85 (total = 3).
- Match: Q → (2) 3
Statement R: If 20 gm of a radioactive substance reduces to 10 gm in 4 minutes, then in what time (in minutes) will 80 gm of the same substance reduce to 20 gm?
- Initial mass = 20 gm → Final mass = 10 gm in 4 minutes.
- This indicates a half-life of 4 minutes.
- 80 gm → 40 gm (4 minutes)
- 40 gm → 20 gm (4 minutes)
4 minutes+4 minutes=8 minutes
- Match: R → (3) 8
Statement S: The mass defect for the nucleus of helium is 0.0302 a.m.u. The binding energy per nucleon for helium in MeV is approximately.
- Mass defect (Δm) = 0.0302 a.m.u.
- 1 a.m.u. = 930 MeV/c².
Binding Energy=Δm×930 MeVA
where A (mass number of helium) = 4.
Binding Energy per nucleon=0.0302×9304≈7 MeV
- Match: S → (4) 7
- P → (1) 8
- Q → (2) 3
- R → (3) 8
- S → (4) 7
Topper's Solved these Questions
Similar Questions
Match the statements given in Column I abd Column II.

View SolutionMatch the statements in Column I with the currnt element in Column II

View SolutionMatch the statement given in Column I with the phenomenon given in Column II.

View SolutionMatch the follwing reactants in Column I with the corresponding reaction products in Column II.

View SolutionMatch the statements given in Column I with the oxidation states given in Column II.

View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionMatch the following item in column I with the corresponding items in Column II.
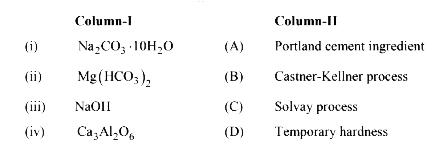
View SolutionMatch the statement of Column I with the values of Column II.
View SolutionMatch the properties given in Column I with the metals given in Column II

View Solution
