A body which was released from rest, slides down on an inclined plane of inclination . The coefficient of friction dowh the plane varies as where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :

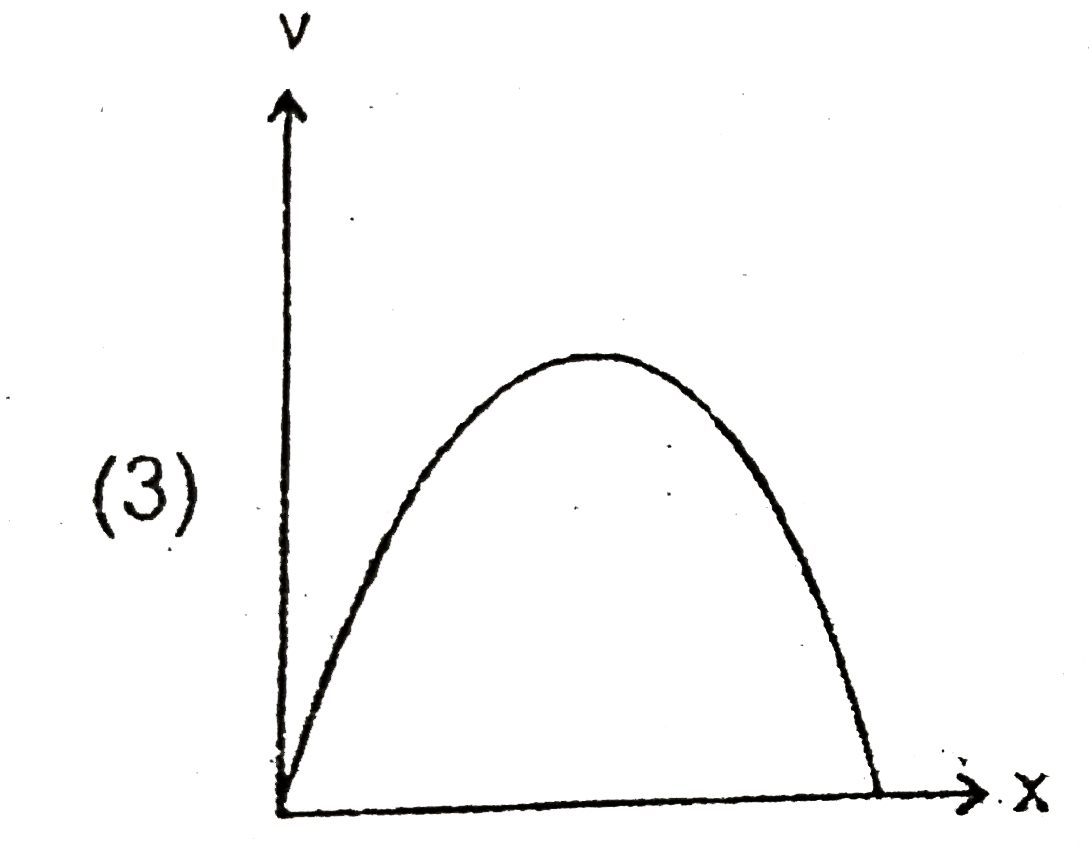
The correct Answer is:C
To solve the problem, we need to analyze the motion of a body sliding down an inclined plane with a varying coefficient of friction. Let's break it down step by step.
Step 1: Identify the forces acting on the body
When the body is on the inclined plane, the following forces act on it:
- Gravitational force (weight) mg
- Normal force N
- Frictional force f
The gravitational force can be resolved into two components:
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
The frictional force, which opposes the motion, is given by:
f=μN
Given that μ=kx, where k is a positive constant and x is the distance moved down the plane, we have:
f=kxN
Step 2: Determine the normal force
The normal force N acting on the body is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Step 3: Write the expression for frictional force
Substituting the expression for N into the frictional force equation:
f=kx(mgcosθ)
Step 4: Apply Newton's second law
The net force acting on the body along the incline is:
Fnet=mgsinθ−f
Substituting the expression for f:
Fnet=mgsinθ−kx(mgcosθ)
Using Newton's second law F=ma, we can write:
ma=mgsinθ−kx(mgcosθ)
Dividing through by m:
a=gsinθ−kx(gcosθ)
Step 5: Relate acceleration to velocity and distance
Acceleration a can also be expressed as:
a=dvdt=dvdx⋅dxdt=vdvdx
Substituting this into our equation gives:
vdvdx=gsinθ−kx(gcosθ)
Step 6: Integrate to find the relationship between v and x
Rearranging the equation:
vdv=(gsinθ−kxgcosθ)dx
Integrating both sides:
∫vdv=∫(gsinθ−kxgcosθ)dx
This results in:
v22=gsinθ⋅x−kgcosθ2x2+C
Step 7: Determine the constant of integration
Since the body is released from rest at x=0 (where v=0):
0=gsinθ⋅0−kgcosθ2⋅02+C⟹C=0
Step 8: Final expression for velocity
Thus, we have:
v2=2gsinθ⋅x−kgcosθ⋅x2
Step 9: Analyze the velocity versus distance graph
The equation v2=2gsinθ⋅x−kgcosθ⋅x2 is a quadratic equation in terms of x. The graph of v versus x will be a parabola that opens downwards (since the coefficient of x2 is negative).
Conclusion
The speed v versus distance x graph will be a downward-opening parabola, indicating that the speed increases to a maximum value and then decreases as the distance x increases.
When the body is on the inclined plane, the following forces act on it:
- Gravitational force (weight) mg
- Normal force N
- Frictional force f
- Perpendicular to the incline: mgcosθ
- Parallel to the incline: mgsinθ
f=μN
Given that μ=kx, where k is a positive constant and x is the distance moved down the plane, we have:
f=kxN
The normal force N acting on the body is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Substituting the expression for N into the frictional force equation:
f=kx(mgcosθ)
The net force acting on the body along the incline is:
Fnet=mgsinθ−f
Substituting the expression for f:
Fnet=mgsinθ−kx(mgcosθ)
ma=mgsinθ−kx(mgcosθ)
Dividing through by m:
a=gsinθ−kx(gcosθ)
Acceleration a can also be expressed as:
a=dvdt=dvdx⋅dxdt=vdvdx
vdvdx=gsinθ−kx(gcosθ)
Rearranging the equation:
vdv=(gsinθ−kxgcosθ)dx
∫vdv=∫(gsinθ−kxgcosθ)dx
This results in:
v22=gsinθ⋅x−kgcosθ2x2+C
Since the body is released from rest at x=0 (where v=0):
0=gsinθ⋅0−kgcosθ2⋅02+C⟹C=0
Thus, we have:
v2=2gsinθ⋅x−kgcosθ⋅x2
The equation v2=2gsinθ⋅x−kgcosθ⋅x2 is a quadratic equation in terms of x. The graph of v versus x will be a parabola that opens downwards (since the coefficient of x2 is negative).
The speed v versus distance x graph will be a downward-opening parabola, indicating that the speed increases to a maximum value and then decreases as the distance x increases.
Topper's Solved these Questions
Similar Questions
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionA body is moving down along inclined plane of angle of inclination q. The coefficient of friction between the body and the plane varies as mu = 0.5x, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by
View SolutionWhen a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA body starts from rest on a long inclined plane of slope 45∘ . The coefficient of friction between the body and the plane varies as μ=0.3x , where x is the distance travelled down the plane. The body will have maximum speed (for g=10m/s2 ) when x =
View SolutionA body weighing 20kg just slides down a rough inclined plane that rises 5 in 12. What is the coefficient of friction ?
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction
 View Solution
View SolutionA small mass slides down an inclined plane of inclination θ with the horizontal the coefficient of friction is μ=μ0x, where x is the distance through which the mass slides down. Then the distance covered by the mass before it stops is
View SolutionWhen a body slides down an inclined plane with coefficient of friction as μk, then its acceleration is given by .
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution

