A block of mass M1 is constrained to move along with a moveable pulley of mass M2 which is connected to a sprin of force constant k, as shown in the figure. If the mass of the fixed pulley is negligible and friction is absent everywhere, then the period of small oscillations of the system is
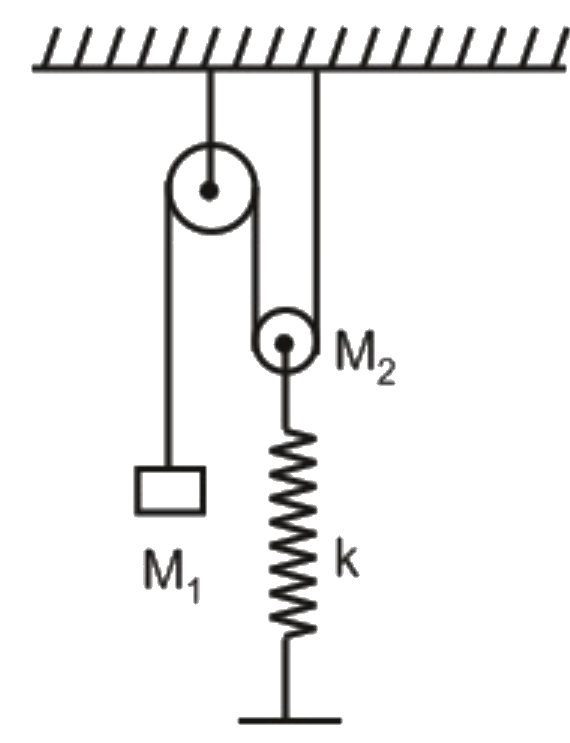
The correct Answer is:T=2π√M2+4M1k

(i) Equilibrium position determination
M1g=T→ (from FBD of M1)
2T=M2g+kx0 (from FBD of M2)
∴2M1g=M2g+kx0
∴kx0=2M1g−M2g
(ii) Displace block M1 by small disp, x by
At new displacement position
−Mgx+12M1V2+12M2(v2)2+M2g(x2)+12K(x0+x2)2x=C
−M1g'dxdt+12M12vdvdt+M282vdvdt+M2g2dxdt+K22(x0+x2)(12dxdt)=0
⇒−M1g+M1a+M2a4+M2g2+K2(x0+x2)=0, (where a=dvdt)
⇒−M1g+M2g2+M1a+M2a4+Kx02+Kx4=0 (from equilibrium −M1g+M2g2+Kx02=0)
Hence, 4M1+M24a=−Kx4
∴a=−K4M1+M2x,ω2=K(4M1+M2)
ω=√K(4M1+M2),T=2πω
∴T2=2π√4M1+M2K
Topper's Solved these Questions
Similar Questions
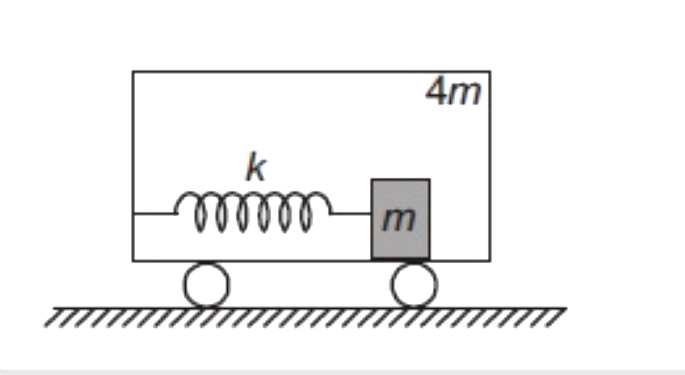
A block of mass m is attached to a cart of mass 4m through spring of spring constant k as shown in the figure. Friction is absent everywhere. The time period of oscillations of the system, when spring is compressed and then released, is
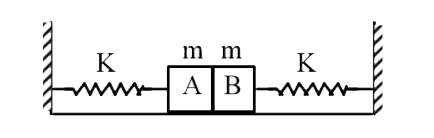
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View Solution
Knowledge Check
A string of negligible mass going over a clamped pulley of mass m supports a block of M as shown in the figure. the force on the pulley by the clamp is given by:
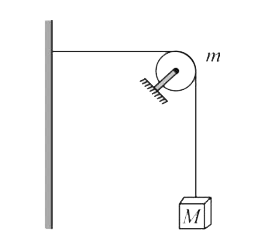 A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A√2MgB√2mgC√(M+m)2+m2gD√(M+m)2+M2g
A block of mass m is arranged on the wedge as shown in figure . The wedge angle is θ. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
View SolutionFind the mass M so that it remains at rest in the abjoining figure. Both the pulley and string are light and friction is absent everywhere. (g=10m/s2)

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionWhat would be the period of the free oscillations of the system shown here if mass M1 is pulled down a little force constant of the spring is k, mass of fixed pulley is negligible and movable pulley is smooth
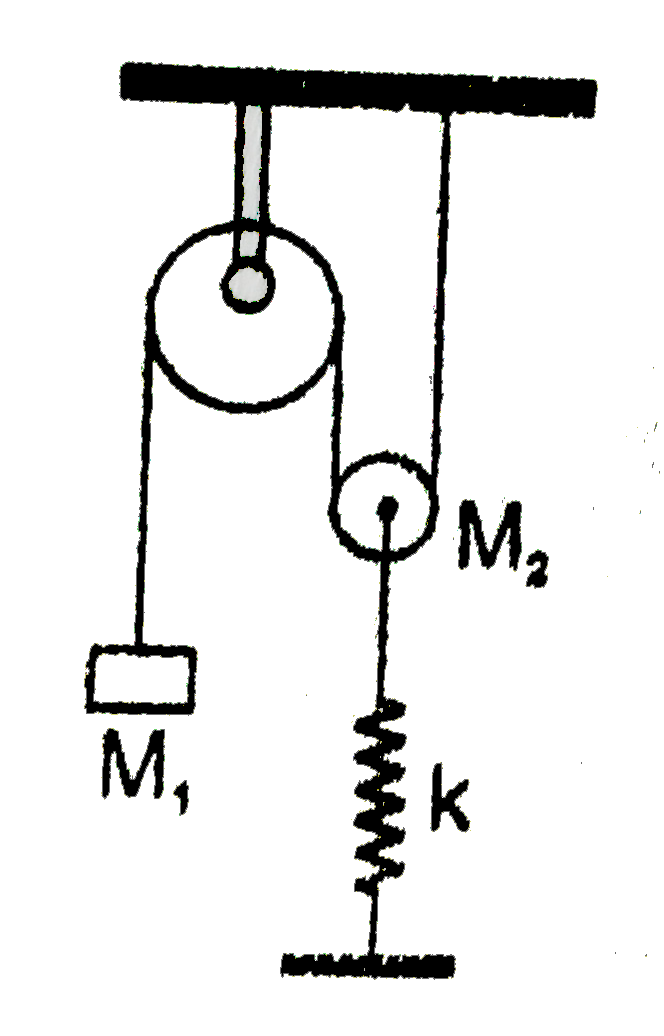
View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View Solution
