Question

The correct graph of $y=\frac{\left|{\log }_{2}x\right|}{{\log }_{2}x}$ is

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem of graphing the function $$y=\frac{|{\log }_{2}x|}{{\log }_{2}x}$$, we will analyze the function step by step.

Step 1: Understanding the Function
The function is defined as:
\( y = \frac{|\log_2 x|}{\log_2 x} \)

Step 2: Determine the Domain
The logarithm function \( \log_2 x \) is defined for \( x > 0 \). Therefore, the domain of the function is \( x > 0 \).

Step 3: Analyze the Sign of \( \log_2 x \)
1. For \( x > 1 \):
- \( \log_2 x > 0 \)
- Thus, \( |\log_2 x| = \log_2 x \)
- Therefore:
\( y = \frac{\log_2 x}{\log_2 x} = 1 \)

2. For \( 0 < x < 1 \):
- \( \log_2 x < 0 \)
- Thus, \( |\log_2 x| = -\log_2 x \)
- Therefore:
\( y = \frac{-\log_2 x}{\log_2 x} = -1 \)

Step 4: Summary of Values
- For \( x > 1 \), \( y = 1 \)
- For \( 0 < x < 1 \), \( y = -1 \)

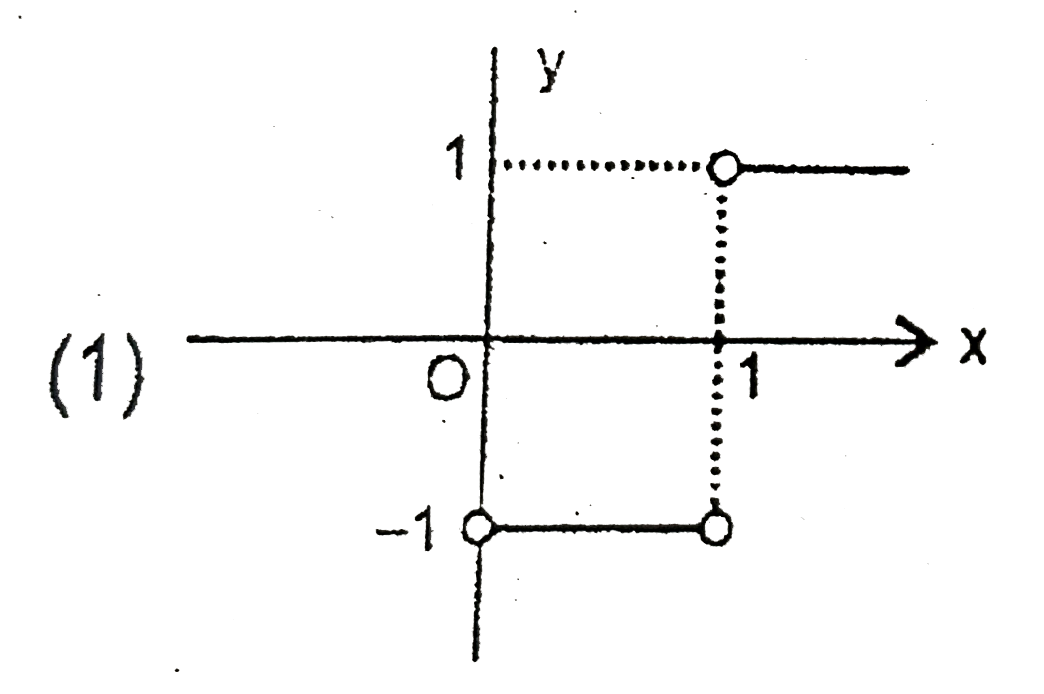
Step 5: Graph the Function
- The graph will have a horizontal line at \( y = 1 \) for \( x > 1 \).
- The graph will have a horizontal line at \( y = -1 \) for \( 0 < x < 1 \).
- At \( x = 1 \), \( \log_2 1 = 0 \) is not defined in the function, so there is a discontinuity at this point.

Step 6: Final Graph
The graph consists of two horizontal lines:
- A line at \( y = 1 \) for \( x > 1 \)
- A line at \( y = -1 \) for \( 0 < x < 1 \)
- There is a discontinuity at \( x = 1 \).

Conclusion
The correct graph of \( y = \frac{|\log_2 x|}{\log_2 x} \) is a piecewise function that takes the value of 1 for \( x > 1 \) and -1 for \( 0 < x < 1 \).

---