A spherical shell of mass M and radius R filed completely with a liquid of same mass and set to rotate about a vertical axis through its centre has a moment of inertia I1 about the axis. The bottom. If moment of inertia of the system is I2 when the shell is half filled and I3 is the moment of inertia when entire water drained off then :
I1I2≈1.5
I1I2≈0.67
I1I3≈1.6
I2I3≈1.4
The correct Answer is:C
To solve the problem, we need to calculate the moment of inertia for three different scenarios involving a spherical shell filled with liquid. We will denote the mass of the shell as M and its radius as R.
Step 1: Calculate I1 (Moment of Inertia when the shell is fully filled)
The moment of inertia of a hollow sphere about an axis through its center is given by:
Ihollow=23MR2
When the shell is filled with liquid of the same mass M, it behaves like a solid sphere. The moment of inertia of a solid sphere is given by:
Isolid=25MR2
Thus, the total moment of inertia I1 when the shell is fully filled is:
I1=Ihollow+Isolid=23MR2+25MR2
To combine these fractions, we find a common denominator (15):
I1=(1015MR2+615MR2)=1615MR2
Step 2: Calculate I2 (Moment of Inertia when the shell is half-filled)
When the shell is half-filled, we treat the system as a hollow hemisphere plus a solid hemisphere of mass M2.
The moment of inertia of a hollow hemisphere is:
Ihollow hemisphere=12Ihollow=12⋅23MR2=13MR2
The moment of inertia of the solid hemisphere is:
Isolid hemisphere=25⋅M2R2=15MR2
Thus, the total moment of inertia I2 when the shell is half-filled is:
I2=Ihollow hemisphere+Isolid hemisphere=13MR2+15MR2
Finding a common denominator (15):
I2=(515MR2+315MR2)=815MR2
Step 3: Calculate I3 (Moment of Inertia when the shell is empty)
When the shell is empty, the moment of inertia is just that of the hollow shell:
I3=23MR2
Step 4: Find the ratios I1I2 and I1I3
Now we can find the ratios:
1. For I1I2:
I1I2=1615MR2815MR2=168=2
2. For I1I3:
I1I3=1615MR223MR2=1615⋅32=16⋅315⋅2=4830=85=1.6
Final Results
- I1=1615MR2
- I2=815MR2
- I3=23MR2
- I1I2=2
- I1I3=1.6
The moment of inertia of a hollow sphere about an axis through its center is given by:
When the shell is half-filled, we treat the system as a hollow hemisphere plus a solid hemisphere of mass M2.
When the shell is empty, the moment of inertia is just that of the hollow shell:
Now we can find the ratios:
- I1=1615MR2
- I2=815MR2
- I3=23MR2
- I1I2=2
- I1I3=1.6
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
The moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a spherical shell and a hemispherical shell of same mass and radius about a tangential axis, passing through P will be

View SolutionA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionWe have a solid sphere and a very thin spheical shell their masses and moments of inertia about a diameter are same. The ratio of their radii will be :
View SolutionTwo spheres of same mass and radius are in contact with each other. If the moment of inertia of a sphere about its diameter is I, then the moment of inertia of both the spheres about the tangent at their common point would be
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
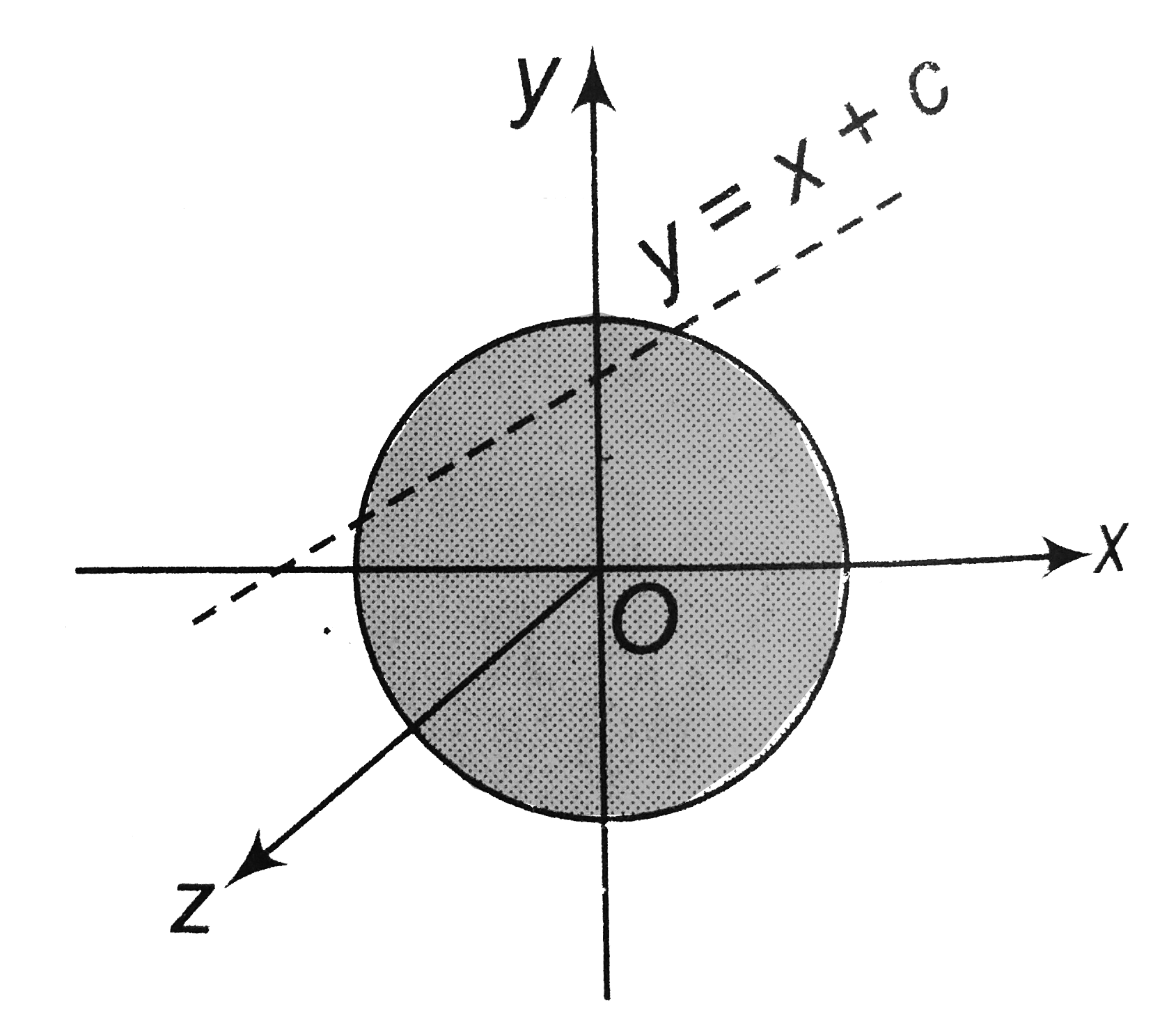 .
.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
View Solution
