Question

Consider a polygon of sides 'n' which satisfies the equation $3\cdot {.}^n{P}_4={.}^{n-1}{P}_5$.
Q. Number of quadrilaterals that can be made using the vertices of the polygon of sides 'n' if exactly two adjacent sides of the quadrilateral are common to the sides of the n-gon is

Options

A. `50`
B. `60`
C. `70`
D. `.^(10)C_(3)-70`

Answer

A::D

Explanation

`3.(n!)/((n - 4)!) = ((n - 1)!)/((n - 6)!), 3n = (n - 4)(n - 5)`
`rArr 3n = n^(2) - 9n + 20 rArr n^(2) - 12n + 20 = 0`
`n = 10, n = 2` , not possible
so `n = 10`

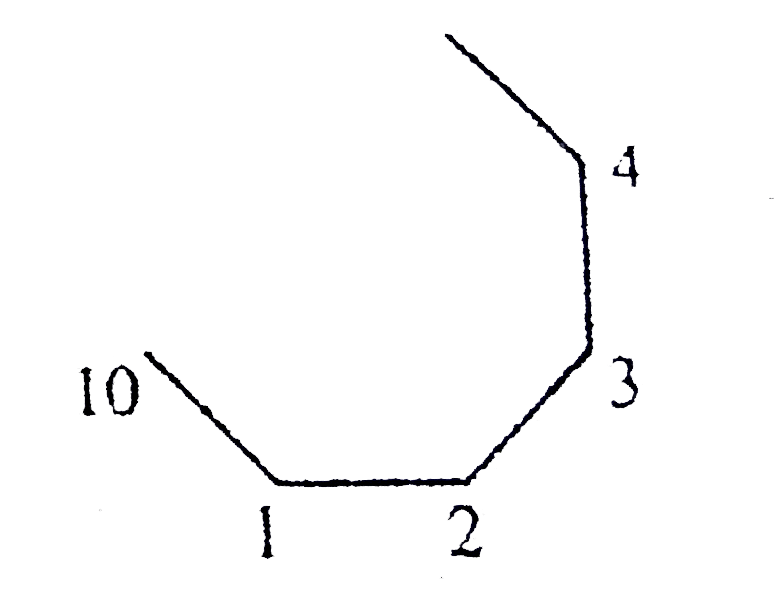
`n = 10`
Consecutive two sides can be formed by `(1, 2, 3)` point `4, 10` can't be selected but one point out of ramain `5` point can be.
selected in `.^(5)C_(1)` ways
So total quadritaterals `= 10x^(5)C_(1) = 50`