Statement-1 : In an e.m. wave magnitude of magnetic field vector →B is much smaller than the magnitude of vector →E
Statement-2 : this is because in and e.m. wave E/B=c=3×108m/s.
Statement-1 is true, statement-2, is true, statement-2 is a correct explanation for statement -1
statement -1 is true, statement -2 is true, statement -2 is NOT a correct explanation for statement -1
statement-1 is true , statement-2 is false
statement-1 is false, statement-2 is true
The correct Answer is:A
To analyze the statements provided in the question, we will break down the concepts related to electromagnetic (e.m.) waves and the relationship between the electric field (E) and magnetic field (B) vectors.
1. Understanding Electromagnetic Waves:
Electromagnetic waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation.
2. Magnitude Relationship:
In an electromagnetic wave, the relationship between the magnitudes of the electric field (E) and the magnetic field (B) is given by the equation:
EB=c
where c is the speed of light in a vacuum, approximately 3×108m/s.
3. Implication of the Relationship:
From the equation E=cB, we can infer that the electric field strength is much greater than the magnetic field strength because c is a very large number. This implies:
E≫B
Thus, the magnitude of the magnetic field vector →B is much smaller than the magnitude of the electric field vector →E.
4. Energy Density in Electromagnetic Fields:
The energy density (energy per unit volume) associated with the electric field UE and magnetic field UB can be expressed as:
UE=12ϵ0E2
UB=12B2μ0
In a given volume, the energy densities of the electric and magnetic fields are equal, leading to the conclusion that:
UE=UB
5. Equating Energy Densities:
By equating the energy densities, we can derive:
12ϵ0E2=12B2μ0
Simplifying this gives:
ϵ0E2=B2μ0
Rearranging yields:
E2B2=1ϵ0μ0
Since 1ϵ0μ0=c2, we have:
EB=c
6. Conclusion:
Therefore, both Statement-1 and Statement-2 are true. However, Statement-2 does not provide a correct explanation for Statement-1. The reason is that while it correctly states the relationship E/B=c, it does not explain why the magnitudes differ.
Final Answer:
- Statement-1: True
- Statement-2: True, but not a correct explanation of Statement-1.
Electromagnetic waves consist of oscillating electric and magnetic fields that are perpendicular to each other and to the direction of wave propagation.
In an electromagnetic wave, the relationship between the magnitudes of the electric field (E) and the magnetic field (B) is given by the equation:
EB=c
where c is the speed of light in a vacuum, approximately 3×108m/s.
From the equation E=cB, we can infer that the electric field strength is much greater than the magnetic field strength because c is a very large number. This implies:
E≫B
Thus, the magnitude of the magnetic field vector →B is much smaller than the magnitude of the electric field vector →E.
The energy density (energy per unit volume) associated with the electric field UE and magnetic field UB can be expressed as:
UE=12ϵ0E2
UB=12B2μ0
In a given volume, the energy densities of the electric and magnetic fields are equal, leading to the conclusion that:
UE=UB
By equating the energy densities, we can derive:
12ϵ0E2=12B2μ0
Simplifying this gives:
ϵ0E2=B2μ0
Rearranging yields:
E2B2=1ϵ0μ0
Since 1ϵ0μ0=c2, we have:
EB=c
Therefore, both Statement-1 and Statement-2 are true. However, Statement-2 does not provide a correct explanation for Statement-1. The reason is that while it correctly states the relationship E/B=c, it does not explain why the magnitudes differ.
- Statement-1: True
- Statement-2: True, but not a correct explanation of Statement-1.
Topper's Solved these Questions
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise
46 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
Similar Questions
A : In an EM wave the magnitude of the electric field vector is more than the magnitude of the magnetic field vector.
R : Energy of the EM wave is shared equally between the electric and magnetic fields.
View Solution(1) In free space at a pont magnitude of electric field vector (→E) is 9.3 V/m. Find the magnitude of magnetic field vector (→B) at the point
(2). Out of ultraviolet infrared and X-rays whose wavelength is maximum ?
View Solution
Knowledge Check
If E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
A→EB→BC→B×→ED→E×→B
(A) : The average magnitude of poynting vector →S is the intensity of electromagnetic wave. (R) : Poynting vector is given by →S=→E×→B2μ0
View SolutionIf E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
View SolutionIf E and B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of eletromagnetic wave is along.
View SolutionTwo vectors →A and →B are added. Prove that the magnitude of the resultant vector cannot be greater than (A+B) and smaller than (A−B) or (B−A).
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
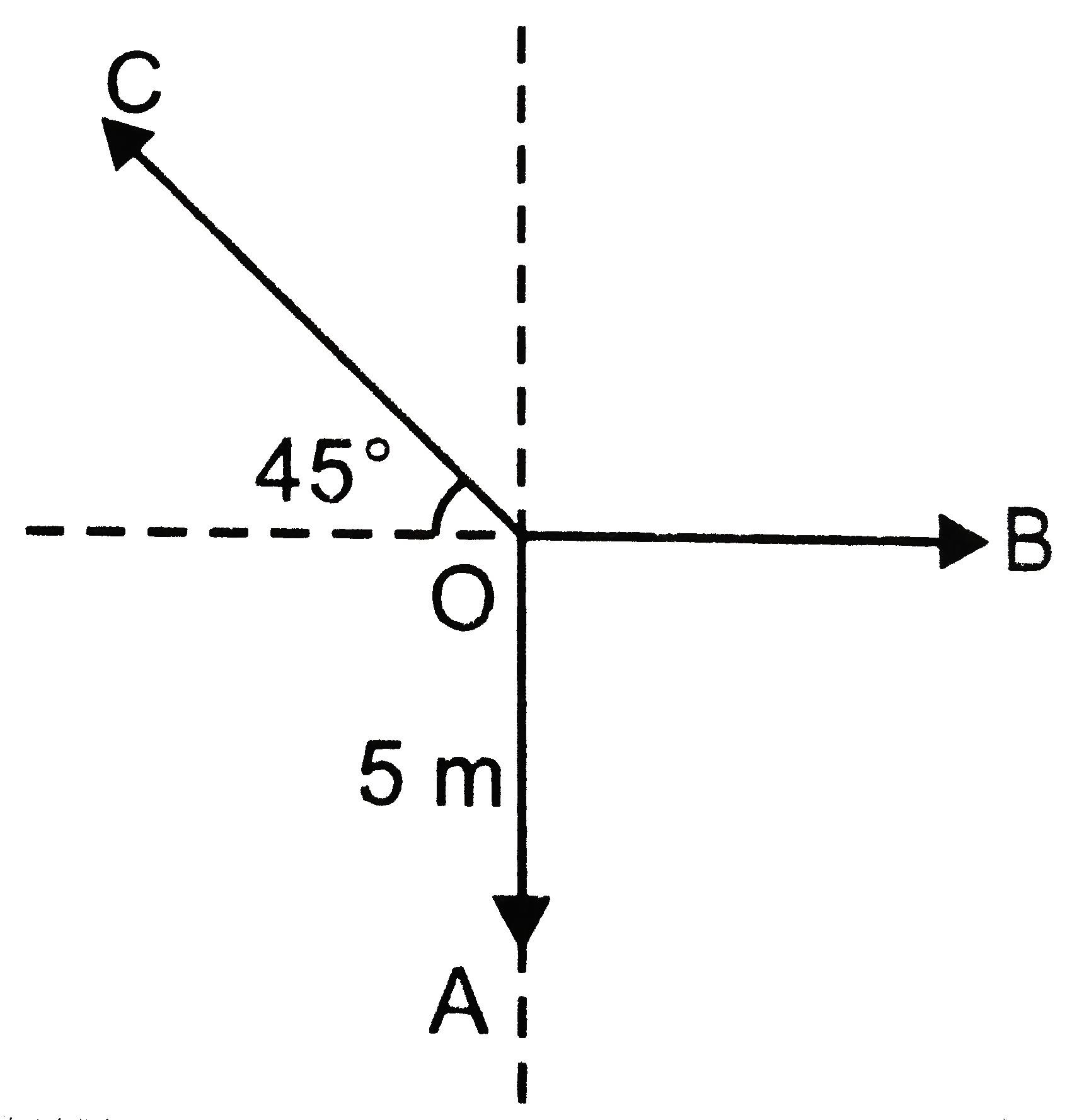 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View SolutionIn electromagnetic wave, the phase difference between electric and magnetic field vectors E and B is
View SolutionIn a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0×1010Hz and amplitude 48V−1m
(a) What is the wavelength o f the wave?
(b) What is the amplitude of the oscillating magnetic field.
(c) Show that the average energy density of the field E equals the average energy density of the field B.[c=3×108ms−1].
View Solution
