If μ and μ2 are the refractive indices of the materials of core and cladding of an optical fibre, then loss of light due to its leakage can be minimised by having
μ1>μ2
μ1<μ2
μ1=μ2
none of these
The correct Answer is:A
To solve the problem regarding minimizing light loss due to leakage in an optical fiber, we need to understand the relationship between the refractive indices of the core and cladding materials.
1. Understanding Optical Fiber Structure:
- An optical fiber consists of two main parts: the core and the cladding. The core is the central part through which light travels, while the cladding surrounds the core and has a lower refractive index.
2. Refractive Indices:
- Let μ1 be the refractive index of the core material.
- Let μ2 be the refractive index of the cladding material.
- For effective light transmission, the refractive index of the core must be greater than that of the cladding, i.e., μ1>μ2.
3. Total Internal Reflection:
- The principle that allows light to be guided through the core of the fiber is called total internal reflection. This phenomenon occurs when light travels from a medium of higher refractive index (core) to a medium of lower refractive index (cladding).
- For total internal reflection to occur, the condition μ1>μ2 must be satisfied.
4. Minimizing Light Loss:
- To minimize the loss of light due to leakage, it is essential to ensure that total internal reflection is maintained. This can be achieved by ensuring that the refractive index of the core is greater than that of the cladding.
- Therefore, the condition μ1>μ2 is necessary to minimize light loss.
5. Conclusion:
- The correct condition to minimize light loss due to leakage in an optical fiber is that the refractive index of the core must be greater than that of the cladding, i.e., μ1>μ2.
Final Answer:
To minimize the loss of light due to its leakage in an optical fiber, it is necessary to have μ1>μ2.
---
- An optical fiber consists of two main parts: the core and the cladding. The core is the central part through which light travels, while the cladding surrounds the core and has a lower refractive index.
- Let μ1 be the refractive index of the core material.
- Let μ2 be the refractive index of the cladding material.
- For effective light transmission, the refractive index of the core must be greater than that of the cladding, i.e., μ1>μ2.
- The principle that allows light to be guided through the core of the fiber is called total internal reflection. This phenomenon occurs when light travels from a medium of higher refractive index (core) to a medium of lower refractive index (cladding).
- For total internal reflection to occur, the condition μ1>μ2 must be satisfied.
- To minimize the loss of light due to leakage, it is essential to ensure that total internal reflection is maintained. This can be achieved by ensuring that the refractive index of the core is greater than that of the cladding.
- Therefore, the condition μ1>μ2 is necessary to minimize light loss.
- The correct condition to minimize light loss due to leakage in an optical fiber is that the refractive index of the core must be greater than that of the cladding, i.e., μ1>μ2.
To minimize the loss of light due to its leakage in an optical fiber, it is necessary to have μ1>μ2.
Topper's Solved these Questions
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 1
40 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
Similar Questions
If μ1andμ2 are the refractive indices of the material of core and cladding respectively of an optical fiber, then
View SolutionA ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
View SolutionLight is incident on the thin lens as shown in figure. The refractive index of the material of the lens is μ2. The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is μ1, while that of right side is μ3. What is the focal length of the lens?

View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionAn optical fibre having core of refractive index √3 and cladding of refractive index 1.5 is kept in air. The maximum angle of acceptance is
View SolutionTwo prisms placed in contact as shown in figure. The condition for net angular dispersion is zero, is (where μf and μv refractive indices of red and voilet light in crown glass respectively and μf'andmu_v' are refractive indices of red and voilet light in flint glass respectively).

View SolutionPulfrich refractometer is used to measure the refractive index of solids and liquid. It consist of right angled prism. A having its two faces perfectly plane. One of the face is horizontal and the other is vertical as shown is figure. The solid B whose refractive index is to be determined is taken having two faces cut perpendicular to one another. Light is incident in a direction parallel to the horizontal surface so that the light entering the prism A is at critical angle C. Finally, it emerges from the prism at an angle i. Let the refractive index of the solid be μ and that of the prism A be μ0 (which is known). Here μ0>μ and by measuring i, μ can be determinged.
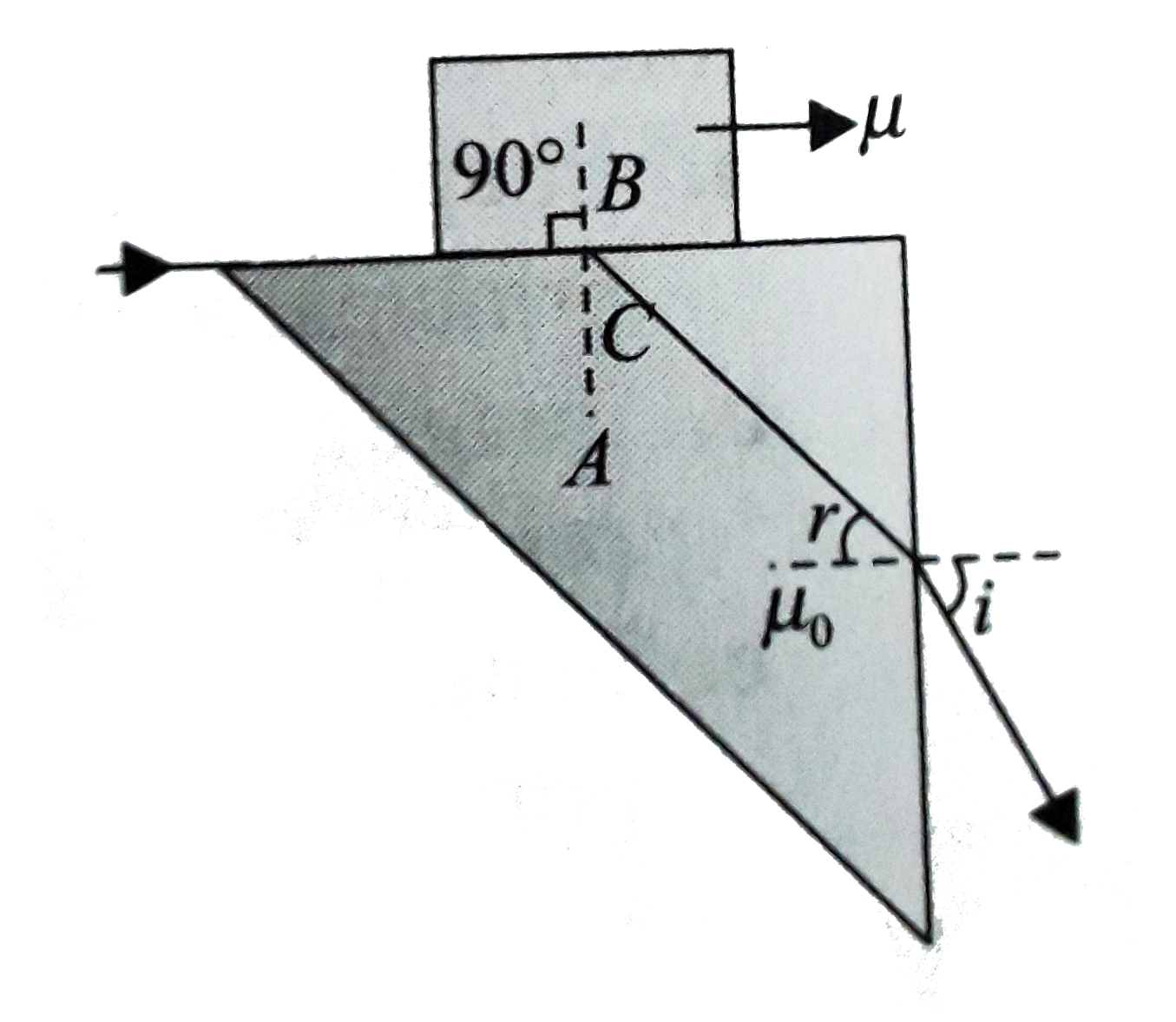
Q. Refractive index of the solid (μ) in terms of μ0 and i is
View SolutionTwo thin slabs of refractive indices μ1 and μ2 are placed parallel to each other in the x-z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj then we have:

View SolutionTwo thin slabs of refractive indices μ1 and μ2 are placed parallel to each other in the x-z plane. If the direction of propagation of a ray in the two media are along the vectors →r1=aˆi+bˆj and →r2=cˆi+dˆj then we have:

View SolutionA thin lens made of a material of refractive indexμ2 has a medium of refractive index μ1 on one side and a medium of refractive index on the other side. The lens is biconvex and the two radii of curvature have equal magnitude R. A beam of light travelling parallel to the principal axis is incident on the lens. Where will the image be formed if the beam is incident from (a) the medium p, and (b) from the medium μ3?
View Solution
