In figure, a cyclic process ABCA of 3 moles of an ideal gas is given. The temperature of the gas at B and C are 500k and 1000K respectively. If work done on the gas in process CA is 2500J then find the net heat absorbed or released by an idela gas. Take R=25/3J/mol−K.
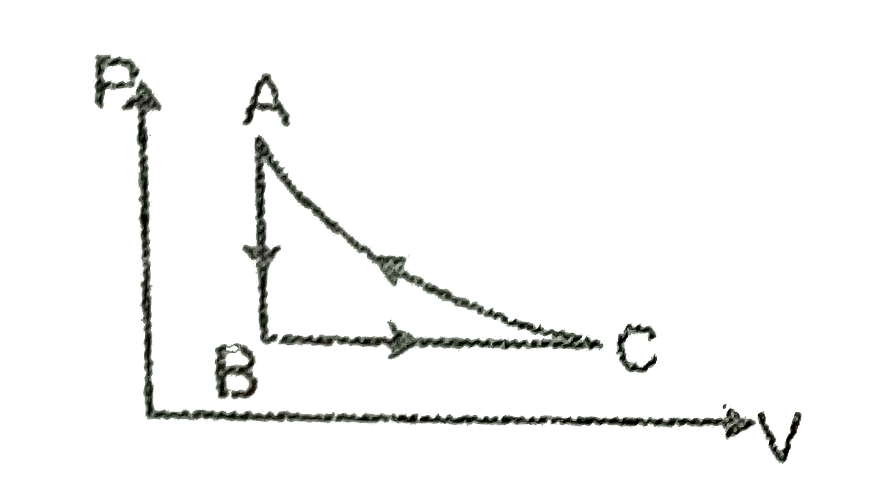
The change in internal energy during the cyclic process is zero. Hence , the heat supplied to the gas is equal to the work done by it. Hence,
ΔQ=WAB+WBC+WCA……….(i)
The work done during the process AB is zero
WBC=PB(VC−VB)
=nR(TC−TB)
=(3mol)(25/3J/mol−K)(500K) ltbr> =12500J
As WCA=−2500J (given)
∴ΔQ=0+12500−2500 [from ..........(i)]
ΔQ=10kJ
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Solved problem
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Problem
3 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - SUBJECTIVE QUESTIONS
27 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
consider the cyclic process ABCA on a sample of 2.0 mol of an ideal gas as shown in the fig. temperature of the gas at A and B are 300 K and 500 k respectively. A total of 1200 J heat is withdrawn from the sample in the process. Find the work done by the gas in part BC. take R=8.3JK−1mol−1

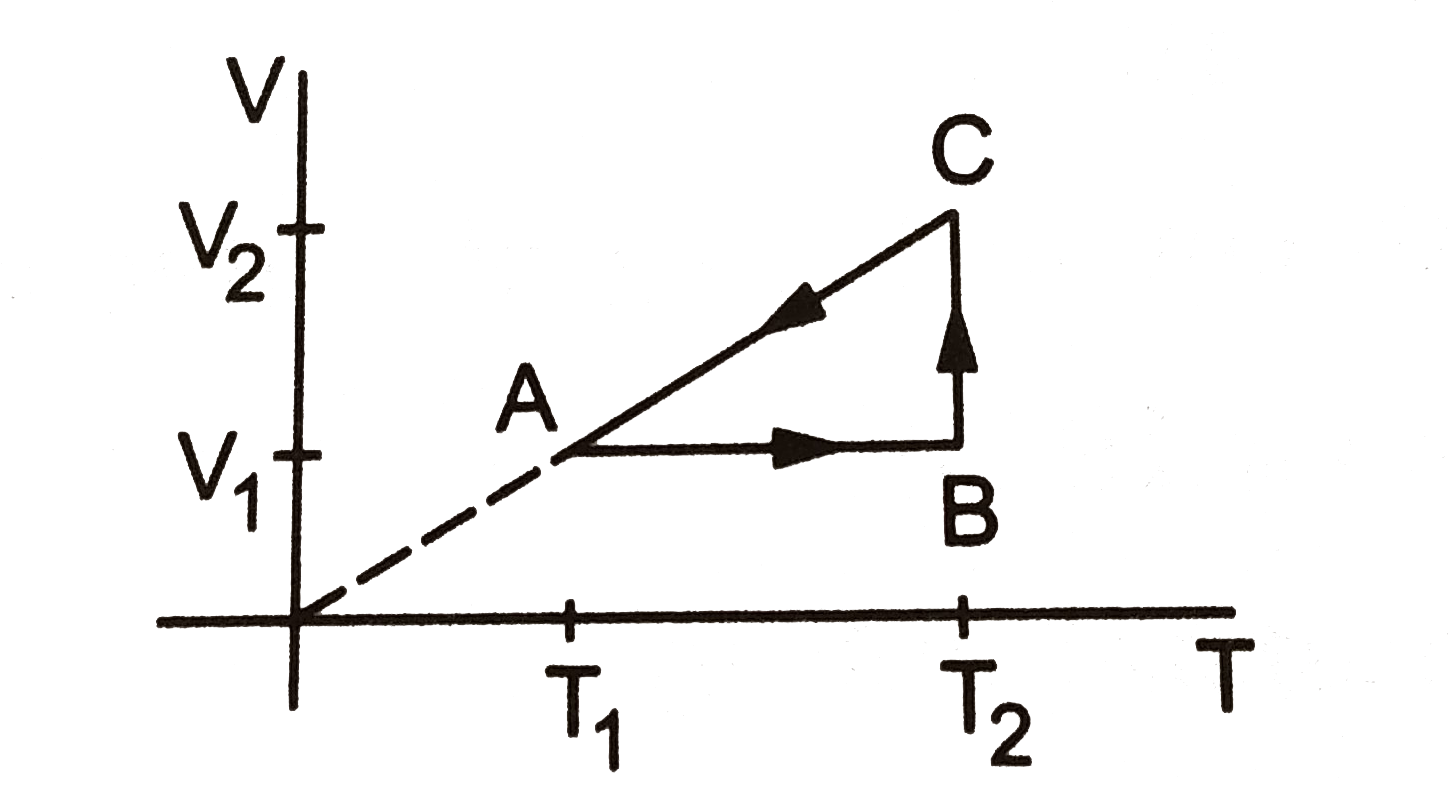
View SolutionThe cyclic process for 1 mole of an ideal gas is shown in the V-T diagram. The work done in AB, BC and CA respectively is

View Solution
Knowledge Check
The cyclic process for 1 mole of an ideal gas is shown in the V-T diagram. The work done in AB, BC and CA respectively is
 A0,RT1Ln(V1V2),R(T1−T2)BR,(T1−T2)R,RT1In(V1V2)C0,RT2ln(V2V1),RT1V1(V1−V2)D0,RT2ln(V1)V2,R(T1−T2)
A0,RT1Ln(V1V2),R(T1−T2)BR,(T1−T2)R,RT1In(V1V2)C0,RT2ln(V2V1),RT1V1(V1−V2)D0,RT2ln(V1)V2,R(T1−T2)
Figure Shows a process ABCA performed on an ideal gas. Find the net heat given to the system during the process.
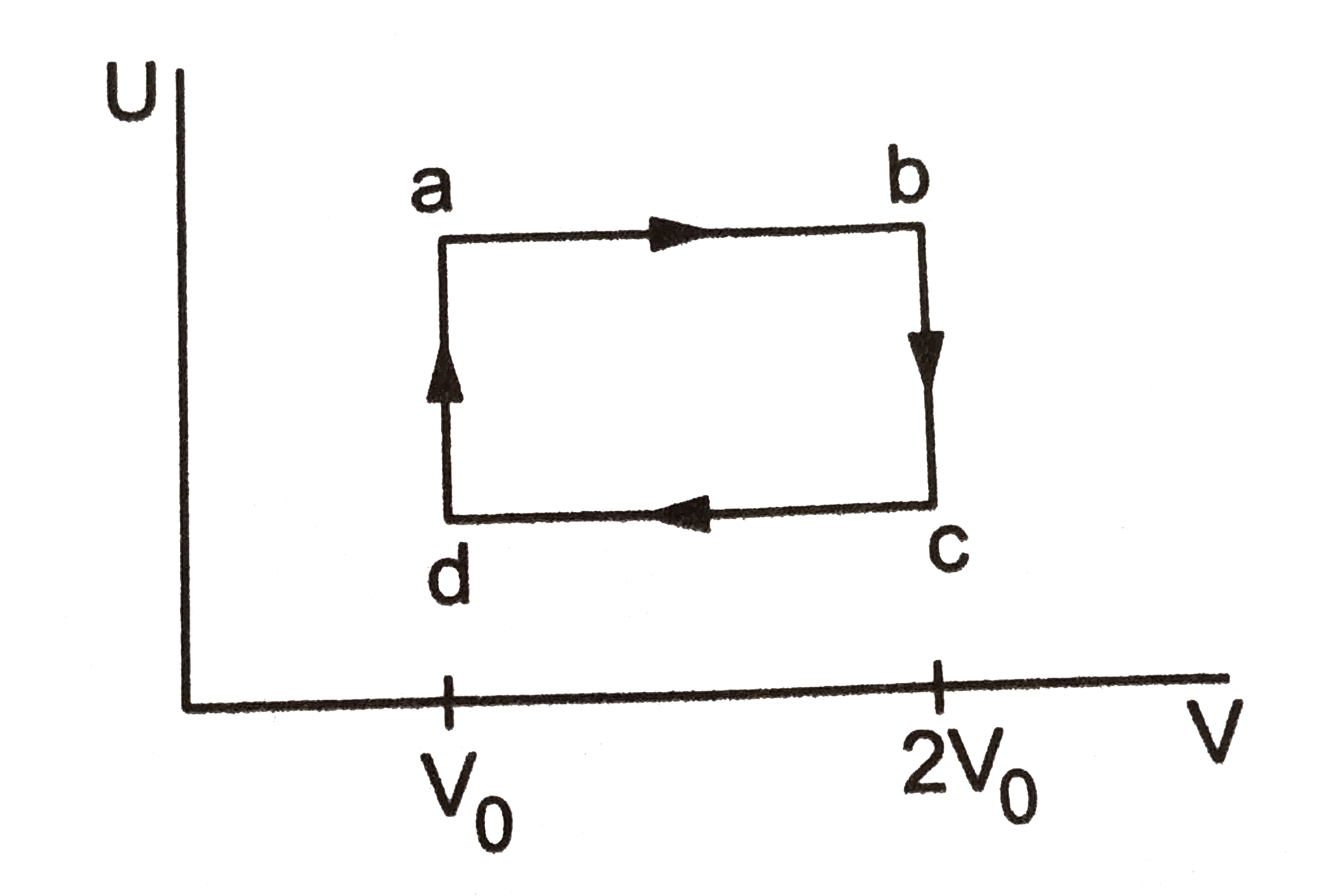
View SolutionFig shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
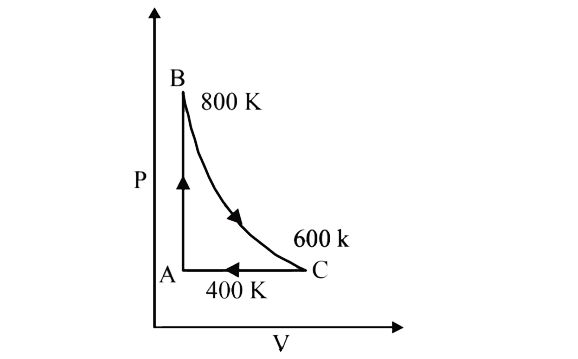
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:

View SolutionTwo moles of an ideal gas are undergone a cyclic process 1-2-3-1. If net heat exchange in the process is 300J, the work done by the gas in the process 2-3 is

View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is
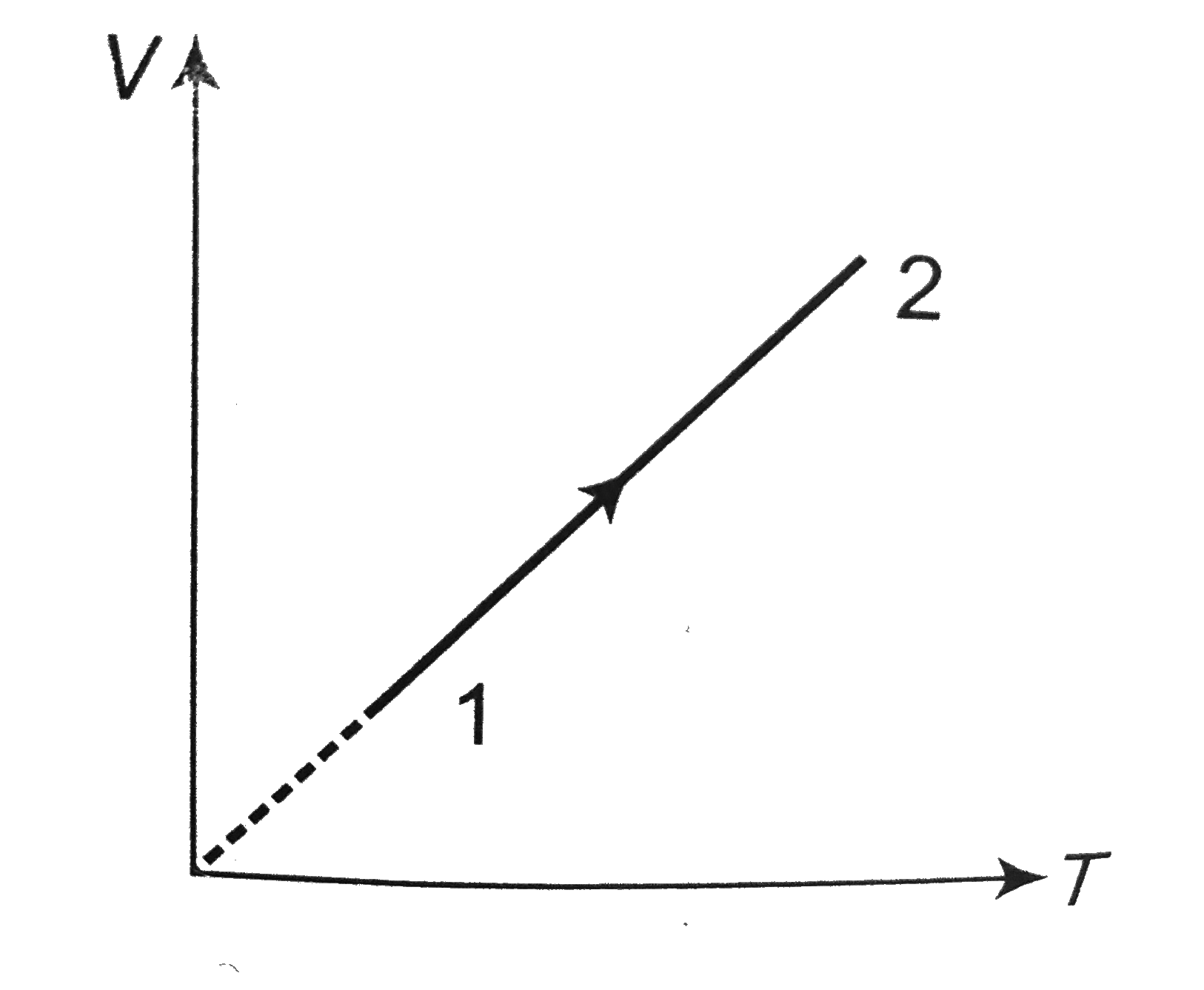
View Solution
