A diatomic gas done 80J work when expanded isobarically. Find the heat given to the gas during this process?
The correct Answer is:280J
To solve the problem of finding the heat given to a diatomic gas during an isobaric expansion where 80 J of work is done, we can follow these steps:
1. Understanding the Process:
The process is isobaric, meaning the pressure (P) remains constant during the expansion of the gas.
2. Using the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
For an isobaric process, we can express the work done (W) as:
W=PΔV
We can also relate the work done to the change in temperature (ΔT) using:
W=nRΔT
3. Finding the Change in Temperature:
Rearranging the equation for work:
ΔT=WnR
Given that W=80J, we can substitute this into the equation:
ΔT=80nR
4. Calculating Change in Internal Energy:
The change in internal energy (ΔU) for a diatomic gas can be expressed as:
ΔU=nCVΔT
For a diatomic gas, CV=52R. Therefore:
ΔU=n(52R)ΔT
Substituting ΔT from the previous step:
ΔU=n(52R)(80nR)
Simplifying this gives:
ΔU=52⋅80=200J
5. Applying the First Law of Thermodynamics:
The first law of thermodynamics states:
ΔQ=ΔU+W
Substituting the values we have:
ΔQ=200J+80J=280J
Final Answer:
The heat given to the gas during this process is:
ΔQ=280J
The process is isobaric, meaning the pressure (P) remains constant during the expansion of the gas.
The ideal gas law is given by the equation:
PV=nRT
For an isobaric process, we can express the work done (W) as:
W=PΔV
We can also relate the work done to the change in temperature (ΔT) using:
W=nRΔT
Rearranging the equation for work:
ΔT=WnR
Given that W=80J, we can substitute this into the equation:
ΔT=80nR
The change in internal energy (ΔU) for a diatomic gas can be expressed as:
ΔU=nCVΔT
For a diatomic gas, CV=52R. Therefore:
ΔU=n(52R)ΔT
Substituting ΔT from the previous step:
ΔU=n(52R)(80nR)
Simplifying this gives:
ΔU=52⋅80=200J
The first law of thermodynamics states:
ΔQ=ΔU+W
Substituting the values we have:
ΔQ=200J+80J=280J
The heat given to the gas during this process is:
ΔQ=280J
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I
15 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -II
17 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
A diatomic gas (γ=1.4) does 200 J of work when it is expanded isobarically. Find the heat given to the gas in the process.
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionFind the work done by the gas in the process ABC.
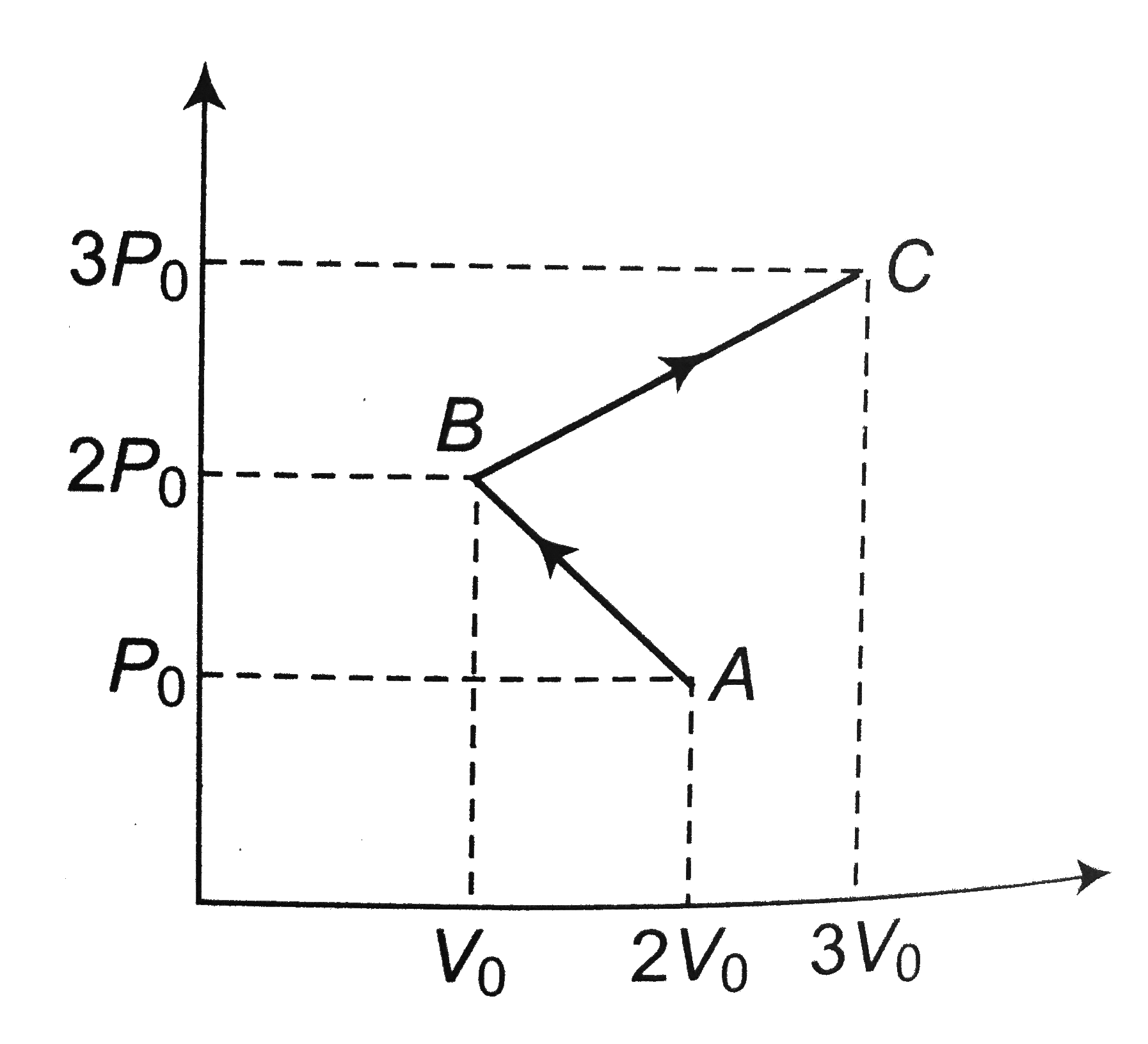
View SolutionWhen heat in given to a gas in an isobaric process, then
View SolutionA diatomic gas with rigid molecules does 10J of work when expanded at constant pressure. The heat energy absorbed by the gas, in this process is ___________ (in J).
View SolutionA diatomic gas with rigid molecules does 10J of work when expanded at constant pressure. The heat energy absorbed by the gas, in this process is ___________ (in J).
View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionP-V curve of a diatomic gas is shown in the Fig. Find the total heat given to the gas in the process A→B→C

View SolutionA diamtomic molecule can be modelled as two rigid balls connected with a spring such that the balls can vibrate with respect to the center of mass of the system ( spring+balls) . Consider a diamtomic gas made of such diatomic molecules. If the gas performs 20 J of work under isobaric condition, then heat given to the gas ( in J ) is
View Solution
