Two moles of an ideal monoatomic gas initially at pressure $P_{1}$ and volume $V_{1}$ undergo an adiabatic compression until its volume is $V_{2}$ . Then the gas is given heat Q at constant volume $V_{2}$ .
(i) Sketch the complete process on a $P - V$ diagram.
(ii) Find the total work done by the gas, the total change in internal energy and the final temperature of the gas. (Give your answer in terms of $P_{1}, V_{1}, V_{2}, Q and R$ )

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $(# # R E S_{H} A T_{P} H Y_{X} I_{C} 01_{E} 01_{298}_A 01 # #)$
$W = \frac{3}{2} P_{1} V_{1} [1 - {(\frac{V_{1}}{V_{2}})}^{2 / 3}]$ ;
$Δ U = Q - W, T_{F} = \frac{Δ U}{3 R} + T_{i} = \frac{Δ U}{3 R} + \frac{P_{1} V_{1}}{2 R}$
$= ⎡ ⎣ \frac{P_{1} V_{1}^{5 / 3} V_{2}^{- 2 / 3}}{2 R} + \frac{Q}{3 R} ⎤ ⎦$

(a) The $P - V$ diagram for the complete process will be as follows:
Process $A \to B$ is adiabatic compression and
Process $B \to C$ is isochoric

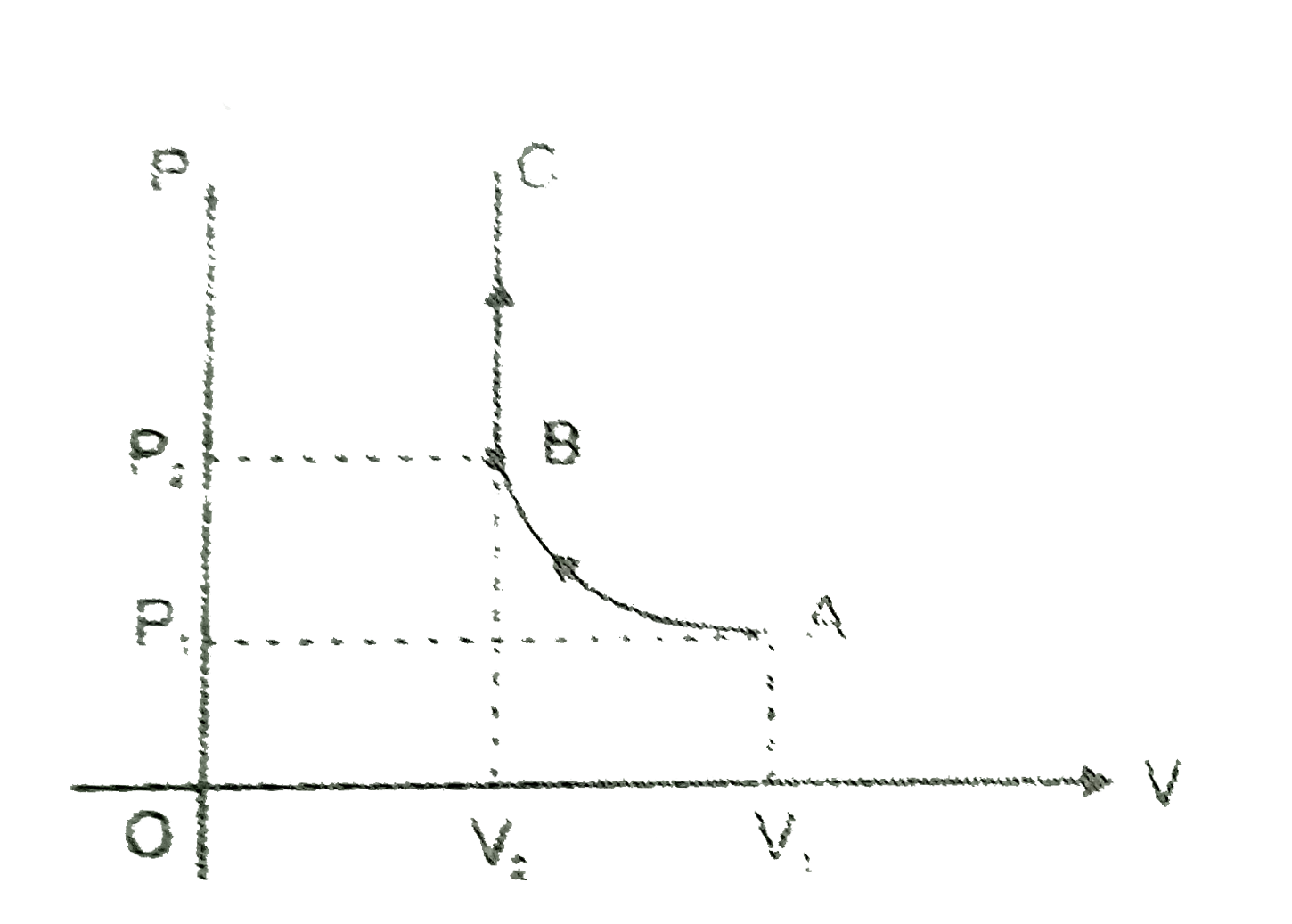
(b) Total work done by the gas Process $A - B$
$W_{adiabatic} = \frac{P_{i} V_{i} - P_{f} V_{f}}{γ - 1}$
$= \frac{P_{1} V_{1} - P_{2} V_{2}}{(5 / 3 - 1)} [γ = 5 / 3$ for monoatomic gas]
$= \frac{P_{1} V_{1} - P_{1} {(\frac{V_{1}}{V_{2}})}^{γ}}{2 / 3} = \frac{3}{2} P_{1} V_{1} [1 - {(\frac{V_{1}}{V_{2}})}^{γ - 1}]$
$⎡ ⎣ \begin{matrix} P_{1} V_{1}^{γ} = P_{2} V_{2}^{γ} ∴ P_{2} = P_{1} {(\frac{V_{1}}{V_{2}})}^{γ} \end{matrix} ⎤ ⎦$
$W = \frac{3}{2} P_{1} V_{1} [1 - {(\frac{V_{1}}{V_{2}})}^{2 / 3}]$
Process $B - C W_{B C} = 0 (V =$ constant)
$∴ W_{Total} = W_{A B} + W_{B C} + \frac{3}{2} P_{1} V_{1} [1 - {(\frac{V_{1}}{V_{2}})}^{2 / 3}]$
(ii) Total change in internal energy
Process $A - B Q_{A B} = 0$ (Process is adiabatic)
$∴ Δ U_{A B} = - W_{A B} = \frac{3}{2} P_{1} V_{1} [{(\frac{V_{1}}{V_{2}})}^{2 / 3} - 1]$
Process $B - C w_{B C} = 0$
$∴ Δ U_{B C} = Q_{B C} = Q$ (Given)
$∴ Δ U_{Total} = Δ U_{A B} + Δ U_{B C} =$ ltbr $\frac{3}{2} P_{1} V_{1} [{(\frac{V_{1}}{V_{2}})}^{2 / 3} - 1] + Q$
(iii) Final temperature of gas
$Δ U_{total} = n C_{v} Δ T = 2 (\frac{R}{γ - 1}) (T_{C} - T_{A})$
$Q + \frac{3}{2} P_{1} V_{1} [{(\frac{V_{1}}{V_{2}})}^{2 / 3} - 1]$
$= \frac{2 R}{(5 / 3 - 1)} (T_{C} - \frac{P_{A} V_{A}}{2 R})$
or $Q + \frac{3}{2} P_{1} V_{1} [{(\frac{V_{1}}{V_{2}})}^{2 / 3} - 1] = 3 R (T_{C} - \frac{P_{1} V_{1}}{2 R})$
$∴ T_{C} = \frac{Q}{3 R} + \frac{P_{1} V_{1}}{2 R} {(\frac{V_{1}}{V_{2}})}^{2 / 3} = T_{final}$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
Aa.179 K
Bb.189 K
Cc.199 K
Dd.219 K

RESONANCE ENGLISH-KTG & THERMODYNAMICS-SUBJECTIVE QUESTIONS

Home
Ask Doubt
Profile