A wooden wheel of radius R is made of two semicircular parts (see figure), The two parts are held together by a ring made of a metal strip of cross sectional area S and length L. L is slightly less than 2πR. To fit the ring on the whell, it is heated so that its temperature rises by ΔT and it just steps over the wheel. As it cools down to surrounding temperature, it presses the semicirular parts together. If te doefficient of linear expansion of the metal is α, and its Youngs' modulus is dY, the force that on part of the wheel applies on the other part is :
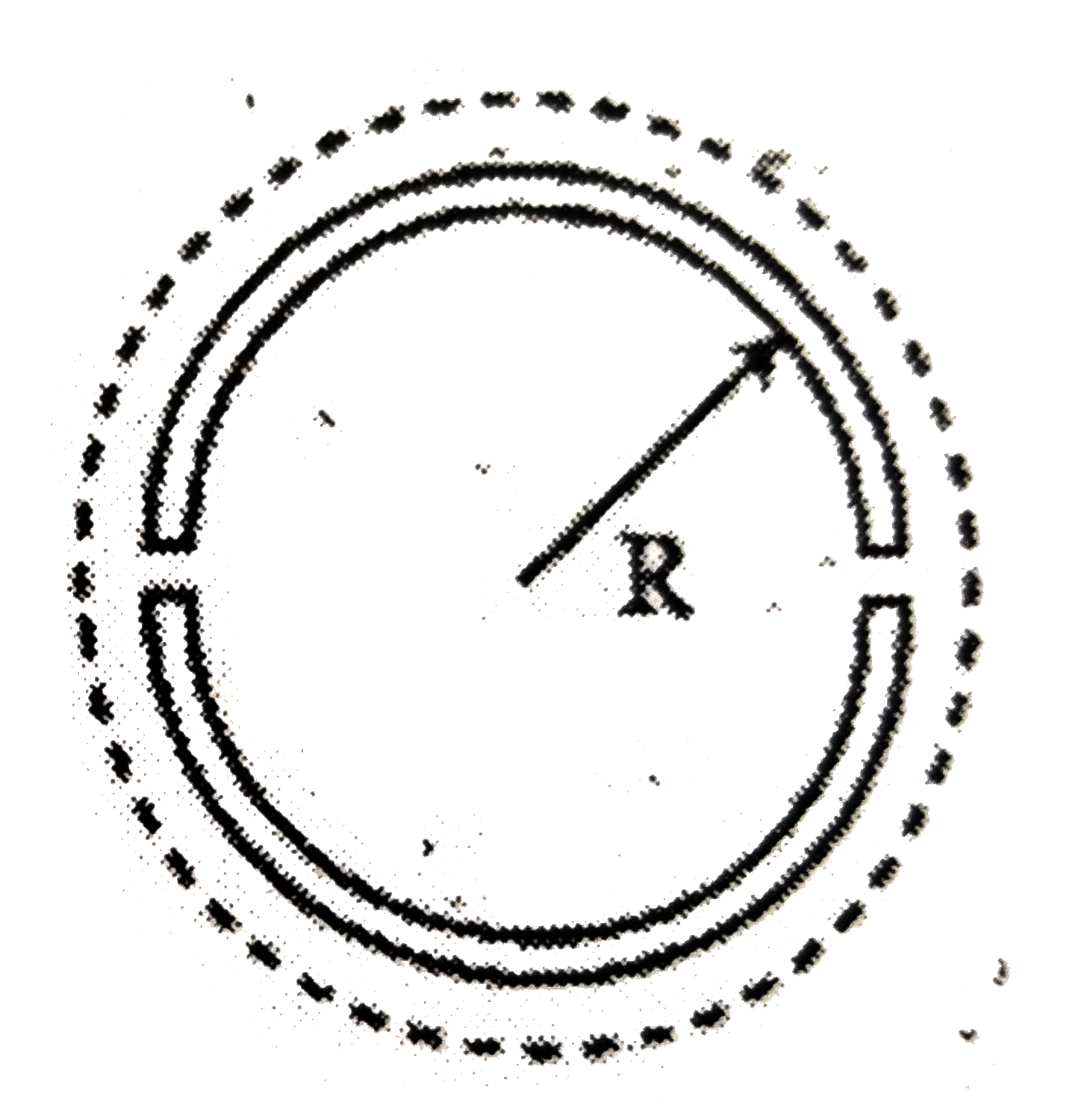
2πSYαΔT
SyαΔT
πSYαΔT
2SYαΔT
The correct Answer is:D

L⇒S
ΔL=L∝ΔT
FA=ΔLLY
F=αΔTYS
So, T=2F
T=2αΔTYS
Topper's Solved these Questions
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Advanced Level Problems
13 Videos
- CALORIMETRY AND THERMAL EXPANSIONBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Exercie-3
1 Videos
- CALORIMETRYBOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise
19 Videos
- CAPACITORBOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise
45 Videos
Similar Questions
A wooden wheel of radius R is made of two semicircular part . The two parts are held together by a ring made of a metal strip of cross sectional area S and length L. L is slightly less than 2πR. To fit the ring on the wheel, it is heated so that its temperature rises by ΔTand it just steps over the wheel. As it cools down to surrounding temperature, it process the semicircle parts together. If the coefficient of linear expansion of the metal is α, and it Young's modulus is Y, the force that one part of the wheel applies on the other part is :

View SolutionTwo wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View SolutionThe length of an iron wire is L and area of cross-section is A. The increase in length is l on applying the force F on its two ends. Which of the statement is correct
View SolutionThe radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View SolutionA uniform ring of radius R and made up of a wire of cross - sectional radius r is rotated about its axis with a frequency f. If density of the wire is ρ and young's modulus is Y . Find the fractional change in radius of the ring .
View SolutionTwo straight metallic strips each of thickness t and length l are rivetted together. Their coefficients of linear expansions areα1andα2. If they are heated through temperature ΔT, the bimetallic strip will bend to form an arc of radius
View SolutionThe radius of a ring is R and its coefficient of linear expansion is α. If the temperature of ring increases by θ then its circumfrence will increase by
View SolutionAn iron tyre is to be fitted onto a wooden wheel 1.0 m in diameter. The diameter of the tyre is 6 mm smaller than that of wheel the tyre should be heated so that its temperature increases by a minimum of (coefficient of volume expansion of iron is 3.6×10−5/∘C)
View SolutionA metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If Youngs modules of metal is Y then tension in the ring is
View Solution
