The velocity of a car moving on a straight road increases linearly accroding to equation, v=1+bx , where a&b are positive constants. The acceleration in the course of such motion :(x is the displacement )
increases
decreases
stay constant
becomes zero
The correct Answer is:A
To solve the problem, we need to find the acceleration of the car given the velocity function v=1+bx, where b is a positive constant and x is the displacement.
1. Identify the given equation:
The velocity of the car is given by the equation:
v=1+bx
2. Understand the relationship between acceleration, velocity, and displacement:
Acceleration a can be expressed in terms of velocity v and displacement x using the formula:
a=vdvdx
Here, dvdx is the derivative of velocity with respect to displacement.
3. Differentiate the velocity function:
To find dvdx, we differentiate v with respect to x:
dvdx=ddx(1+bx)=b
Since b is a constant, the derivative is simply b.
4. Substitute v and dvdx into the acceleration formula:
Now, we can substitute v and dvdx into the acceleration formula:
a=vdvdx=(1+bx)⋅b
5. Expand the expression:
Expanding the expression gives:
a=b+b2x
6. Analyze the result:
The expression a=b+b2x shows that the acceleration is a function of displacement x. Since b is a positive constant, b2 is also positive. Therefore, as x increases, the term b2x increases, which means that the acceleration a increases as x increases.
Final Answer:
The acceleration of the car increases with displacement.
The velocity of the car is given by the equation:
v=1+bx
Acceleration a can be expressed in terms of velocity v and displacement x using the formula:
a=vdvdx
Here, dvdx is the derivative of velocity with respect to displacement.
To find dvdx, we differentiate v with respect to x:
dvdx=ddx(1+bx)=b
Since b is a constant, the derivative is simply b.
Now, we can substitute v and dvdx into the acceleration formula:
a=vdvdx=(1+bx)⋅b
Expanding the expression gives:
a=b+b2x
The expression a=b+b2x shows that the acceleration is a function of displacement x. Since b is a positive constant, b2 is also positive. Therefore, as x increases, the term b2x increases, which means that the acceleration a increases as x increases.
The acceleration of the car increases with displacement.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP NO. 14 PHYSICS10videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 158videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no 12 Physics8videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
The velocity of a particle along a straight line increases according to the linear law v=v0+kx, where k is a constant. Then
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V-t graph.
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionThe velocity varies with time as →v=aˆi+btˆj , where a and b are positive constants. The magnitude of instantaneous velocity and acceleration would be
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
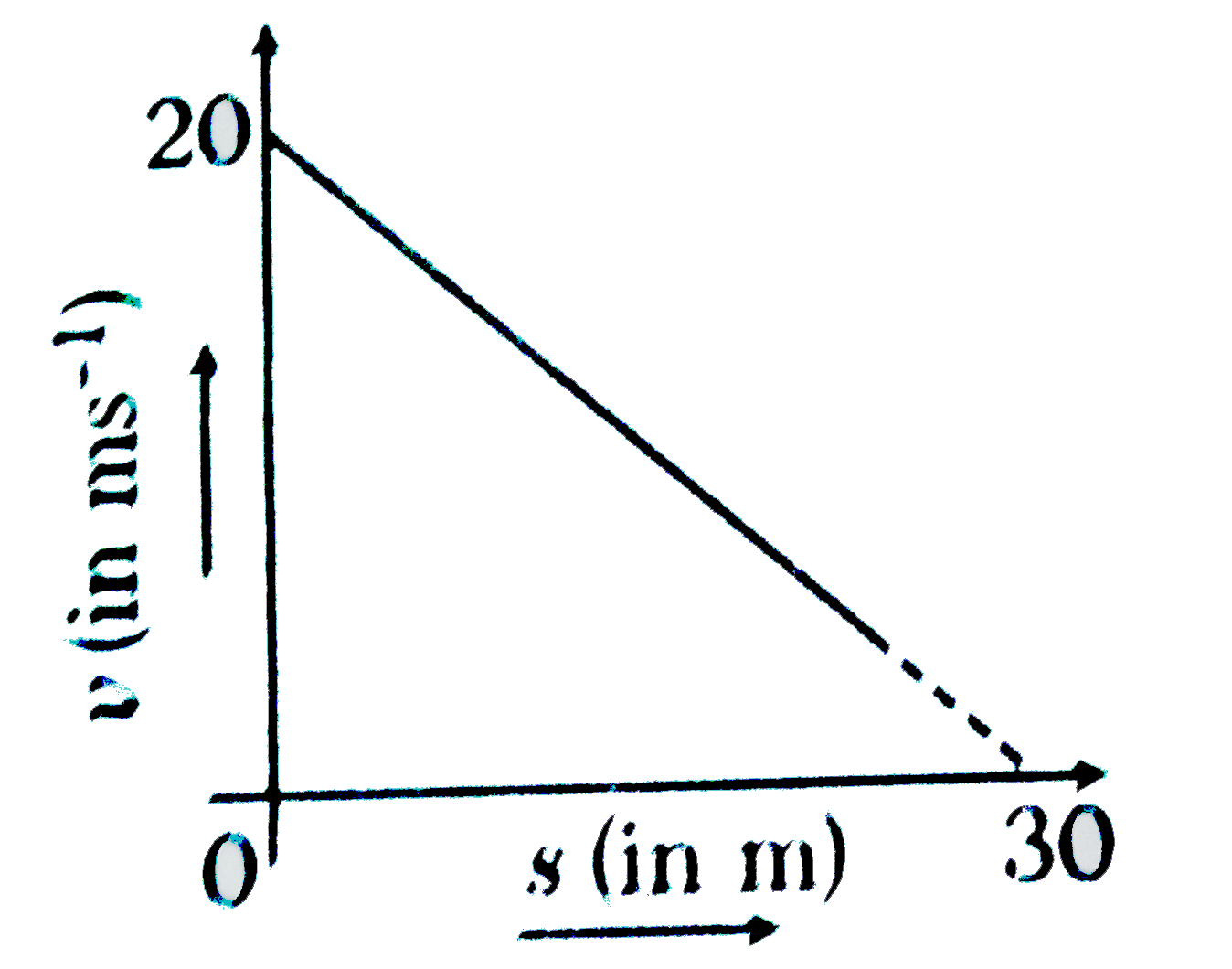 View Solution
View SolutionA particle constrained to move along x-axis given a velocity u along the positive x-axis. The acceleration ' a ' of the particle varies as a = - bx, where b is a positive constant and x is the x co-ordinate of the position of the particle . Then select the correct alternative(s): .
View SolutionA projectile is fired with speed v0 at t=0 on a planet named ' Increasing Gravity ' . This planet is strange one, in the sense that the acceleration due to gravity increases linearly with time t asg(t)=bt, where b is a positive constant. 'Increase Gravity'.
If angle of projection with horizontal is θ then the time of flight is :View SolutionA projectile is fired with speed v0 at t=0 on a planet named ' Increasing Gravity ' . This planet is strange one, in the sense that the acceleration due to gravity increases linearly with time t asg(t)=bt, where b is a positive constant. 'Increase Gravity'
If angle of projection with horizontal is θ, then the maximum height attained isView SolutionThe velocity of a particle moving on the x-axis is given by v=x2+x, where x is in m and v in m/s. What is its position (in m) when its acceleration is 30m/s2.
View Solution

