The velocity of a particle along a straight line increases according to the linear law , where k is a constant. Then
The acceleration of the particle is
The particle takes a time In to attain a speed of v
Velocity varies linearly with displacement with slope of velocity-displacement curve equal to k
Data is In suffiecent to arrives at a conclusion.
The correct Answer is:a,b,c
Further a=
In
Similar Questions
If a particle is moving along straight line with increasing speed, then
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
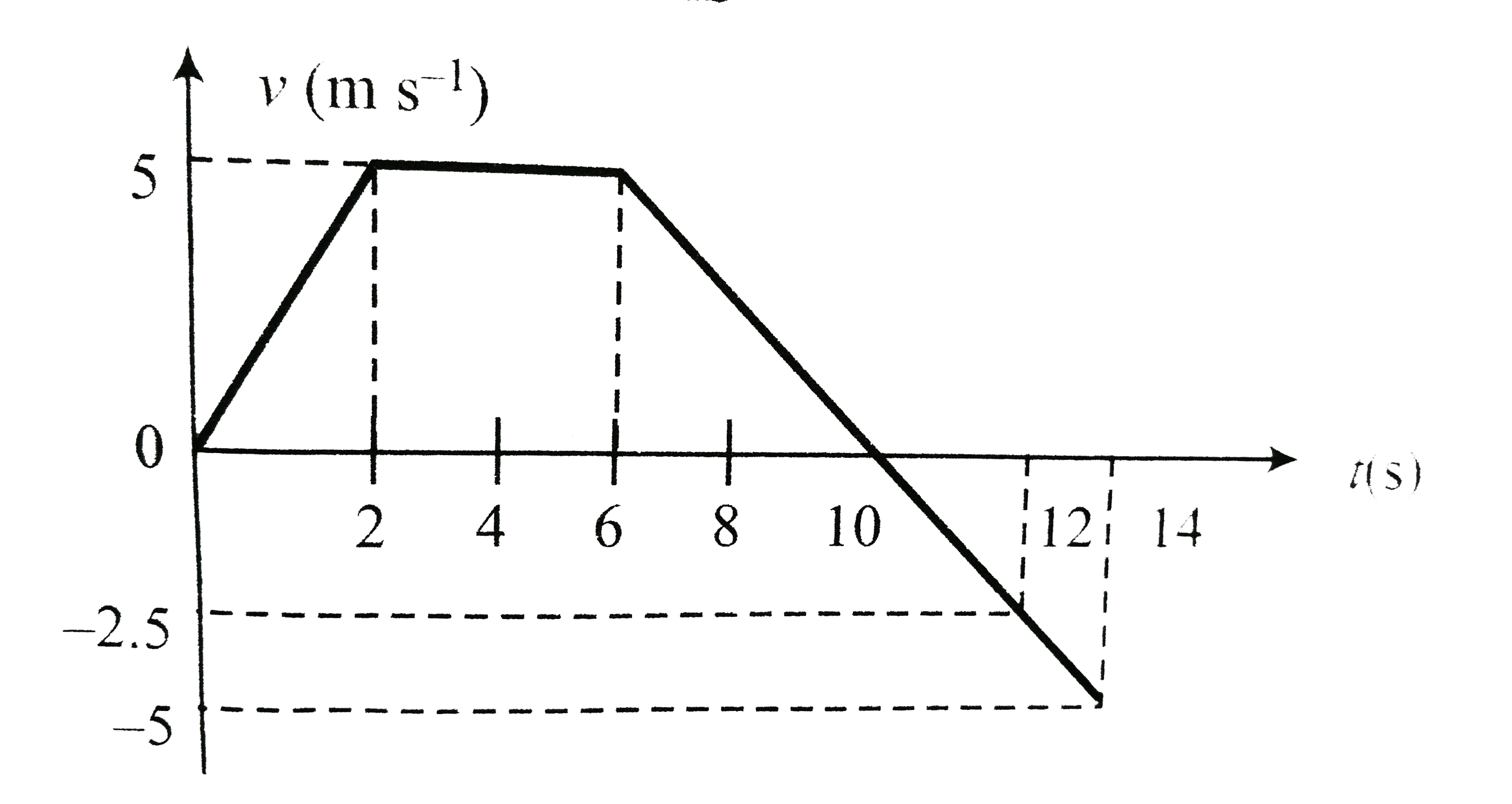 .
.
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of time
View SolutionThe instantaneous velocity of a particle moving in a straight line is given as a function of time by: v=v0(1−(tt0)n) where t0 is a constant and n is a positive integer . The average velocity of the particle between t=0 and t=t0 is 3v04.Then , the value of n is
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V-t graph.
View SolutionThe velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionThe velocity v of a particle of mass is moving along a straight line change with time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View Solution
