A man moves on his motorbike with 54km/h and then takes a U-turn and containues to move with same velocity The time of U-turn is 10s. Find the magnitude of average acceleration during U-turn.
0
3ms−2
1.5√2ms−2
none of these
The correct Answer is:B
To find the magnitude of average acceleration during the U-turn, we can follow these steps:
Step 1: Convert the speed from km/h to m/s
The speed of the motorbike is given as 54 km/h. We need to convert this to meters per second (m/s) using the conversion factor 1 km/h=518 m/s.
Speed in m/s=54×518=15 m/s
Step 2: Identify initial and final velocities
When the man takes a U-turn, he initially moves in one direction and then turns around to move in the opposite direction.
- Initial velocity (v_initial): When moving in the positive direction, we can represent this as +15 m/s.
- Final velocity (v_final): After the U-turn, he moves in the opposite direction, which can be represented as −15 m/s.
Step 3: Calculate the change in velocity
The change in velocity (Δv) can be calculated as:
Δv=vfinal−vinitial=(−15 m/s)−(15 m/s)=−30 m/s
Step 4: Calculate average acceleration
Average acceleration (aavg) is defined as the change in velocity divided by the time taken for that change. The time taken for the U-turn is given as 10 seconds.
aavg=ΔvΔt=−30 m/s10 s=−3 m/s2
Step 5: Find the magnitude of average acceleration
The magnitude of average acceleration is the absolute value of the average acceleration:
Magnitude of aavg=|−3 m/s2|=3 m/s2
Final Answer
The magnitude of average acceleration during the U-turn is 3 m/s2.
---
The speed of the motorbike is given as 54 km/h. We need to convert this to meters per second (m/s) using the conversion factor 1 km/h=518 m/s.
When the man takes a U-turn, he initially moves in one direction and then turns around to move in the opposite direction.
- Final velocity (v_final): After the U-turn, he moves in the opposite direction, which can be represented as −15 m/s.
The change in velocity (Δv) can be calculated as:
Average acceleration (aavg) is defined as the change in velocity divided by the time taken for that change. The time taken for the U-turn is given as 10 seconds.
The magnitude of average acceleration is the absolute value of the average acceleration:
The magnitude of average acceleration during the U-turn is 3 m/s2.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 15
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 16 physics
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no. 13 physics
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
An athelete takes 2.0 s to reach his maximum speed of 18.0 km/h. What is the magnitude of his average acceleration?
View SolutionA proton in a cyclotron changes its velocity from 30 kms–1 the north of 40 kms–1 the east in 20 s. What is the magnitude of average acceleration during this time ?
View Solution
Knowledge Check
A man walks on a straight road from his home to a market 2.5km away with a speed of 5km/h. Finding the market closed, he instantly turns and walks back with a speed of 7.5km/h. What is the (a) magnitude of average velocity and (b) average speed of the man, over the interval of time (i) 0 to 30 min . (ii) 0 to 50 min (iii) 0 to 40 min ?
A0,0B6kmh−1,0C0, 6km−1D6kmh−1,6kmh−1
When a motor cyclist takes a U-turn in 4s what is the average angular velocity of the motor cyclist?
View SolutionA car is moving in east direction. It takes a right turn and moves along south direction without change in its speed. What is the direction of average acceleration of the car?
View SolutionFrom a point on the ground a particle is projected with initial velocity u, such that its horizontal range is maximum. The magnitude of average velocity during its ascent is
View SolutionA particle is moving eastwards with a speed of 6 m/s. After 6 s, the particle is found to be moving with same speed in a direction 60∘ north of east. The magnitude of average acceleration in this interval of time is
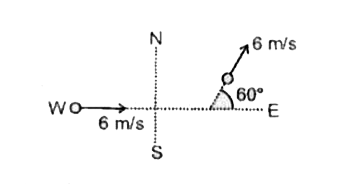
View SolutionA man walks on a straight road from his home to market 2.5 km away with speed of 5 km/h Finding the market closed, he instantly turns and walks back with a speed of 7.5 km/h. What is the magnitude of average velocity and average speed of the man over the interval of time (i) 0 to 30 min (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionAn athlete, initially at rest, takes 2 s to reach his maximum speed of 36 km h−1. The magnitude of his average accleration (inms−2) is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
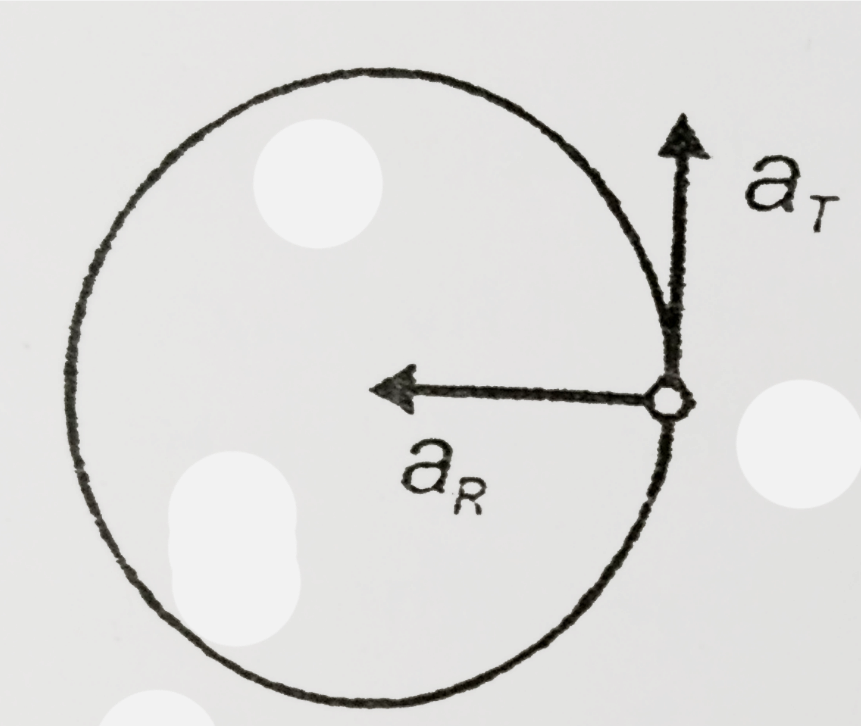
The magnitude of tangential acceleration at t=R2u is
View Solution
