In the figure at the free end a force F is applied to keep the suspended mass of 18 kg at rest. The value of F is :
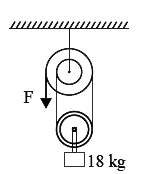
60N
120N
180N
240N
The correct Answer is:D

3F=180
F=60N
T=4F=210N
Force balance on system
T=F+180
T=60+18=240N.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - TRUE/FALSE
2 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 25
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp23
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
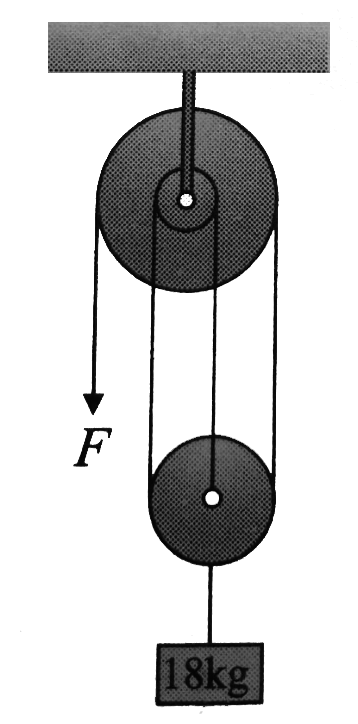
In the figure, at the free end of the light string, a force F is supplied to keep the suspended mass of 18 kg at rest. Then the force exerted by the ceiling on the system (assume that the string segments are vertical and the pulleys are light and smooth) is:(g=10ms2)
View Solution
In the figure shown, a force F is applied at the top of a disc of mass 4 kg and radius 0.25 m. find maximum velue of F for no slipping.
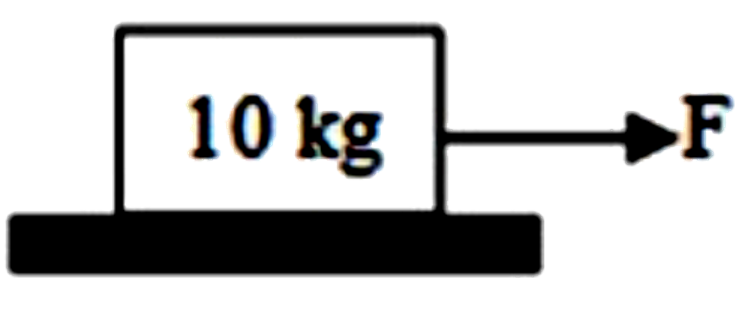
View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
View SolutionA wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

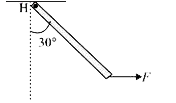
View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
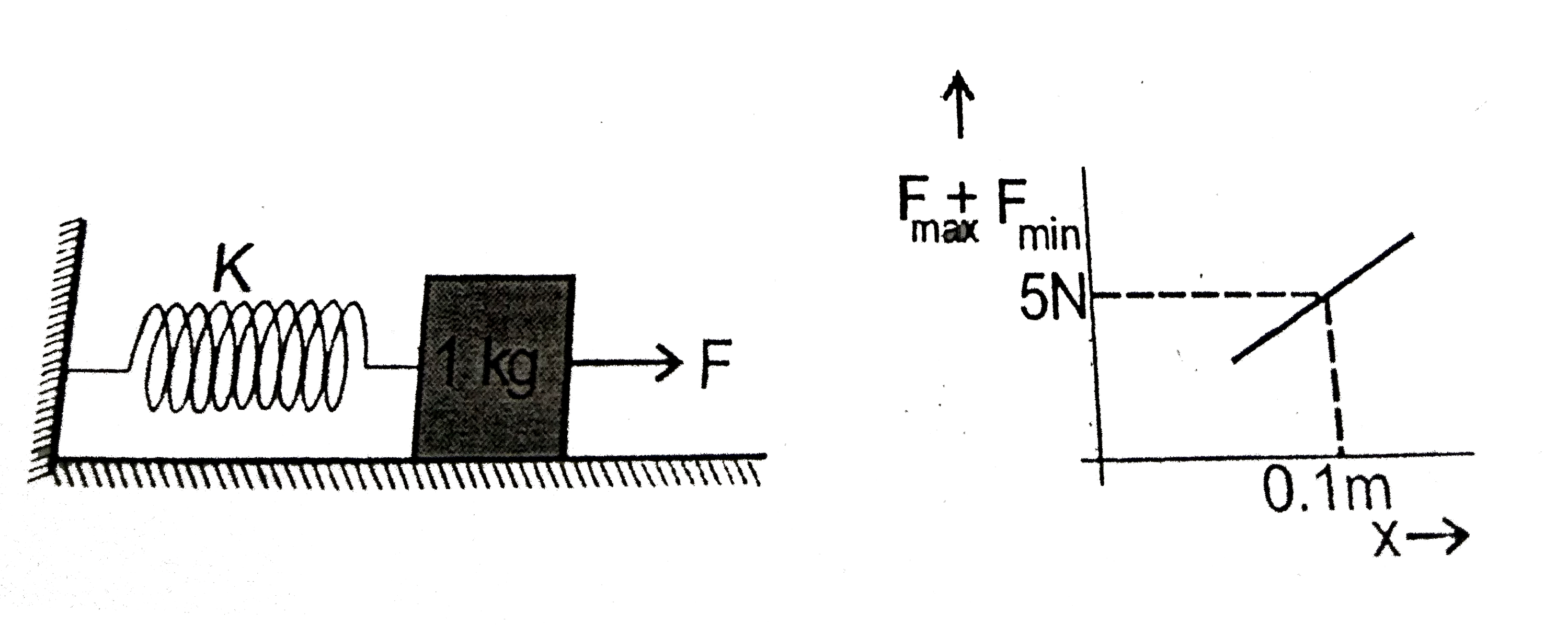
The value of Fmin, if x=3cm is :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
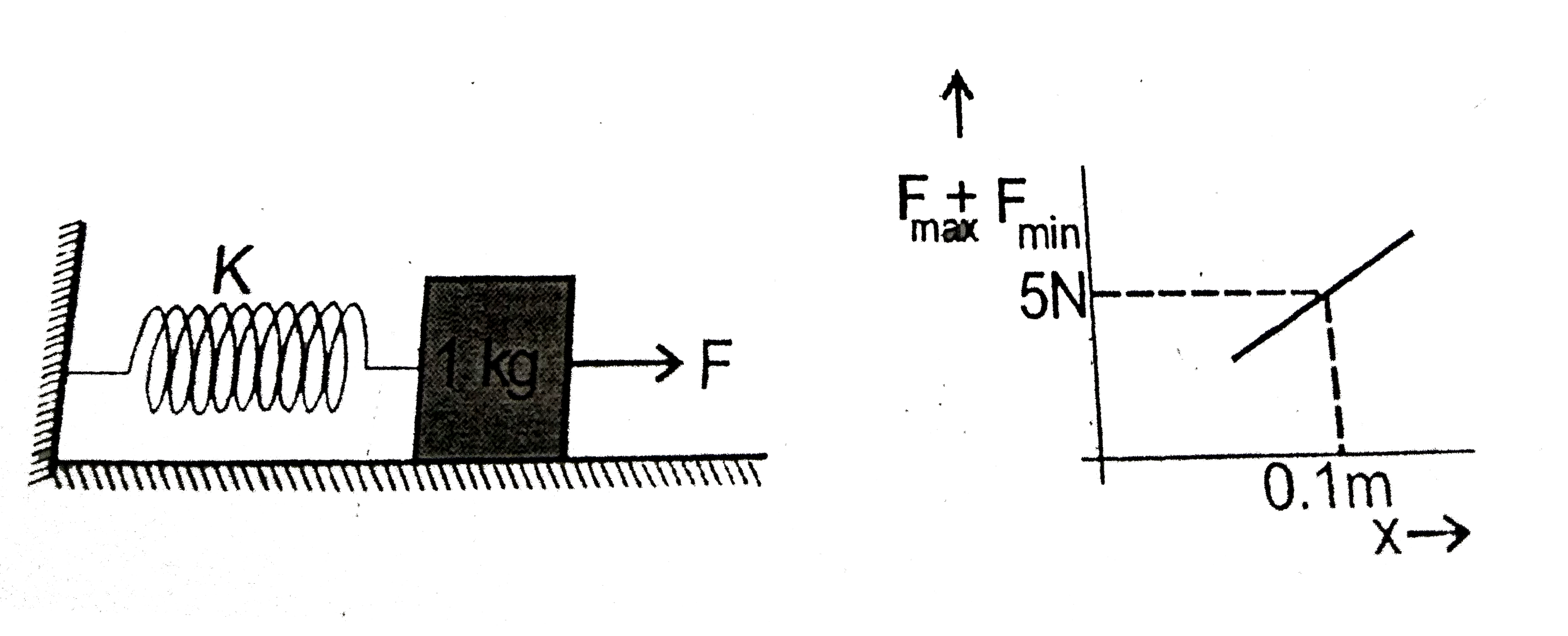
The coefficient of friction between the block and the horizontal surface is :
View SolutionA block of mass 1kgis placed on a rough horizontal surface. A spring is attached to the block whose other end is joined to a rigid wall, as shown in the figure. A horizontal force is applied on the block so that it remains at rest while the spring is elongated by x(x≥μmgk). Let Fmax and Fmin be the maximum and minimum values of force F for which the block remains in equilibrium. For a particular x,Fmax−Fmin=2N. Also shown is the variation of Fmax+Fmin versus x, the elongation of the spring.
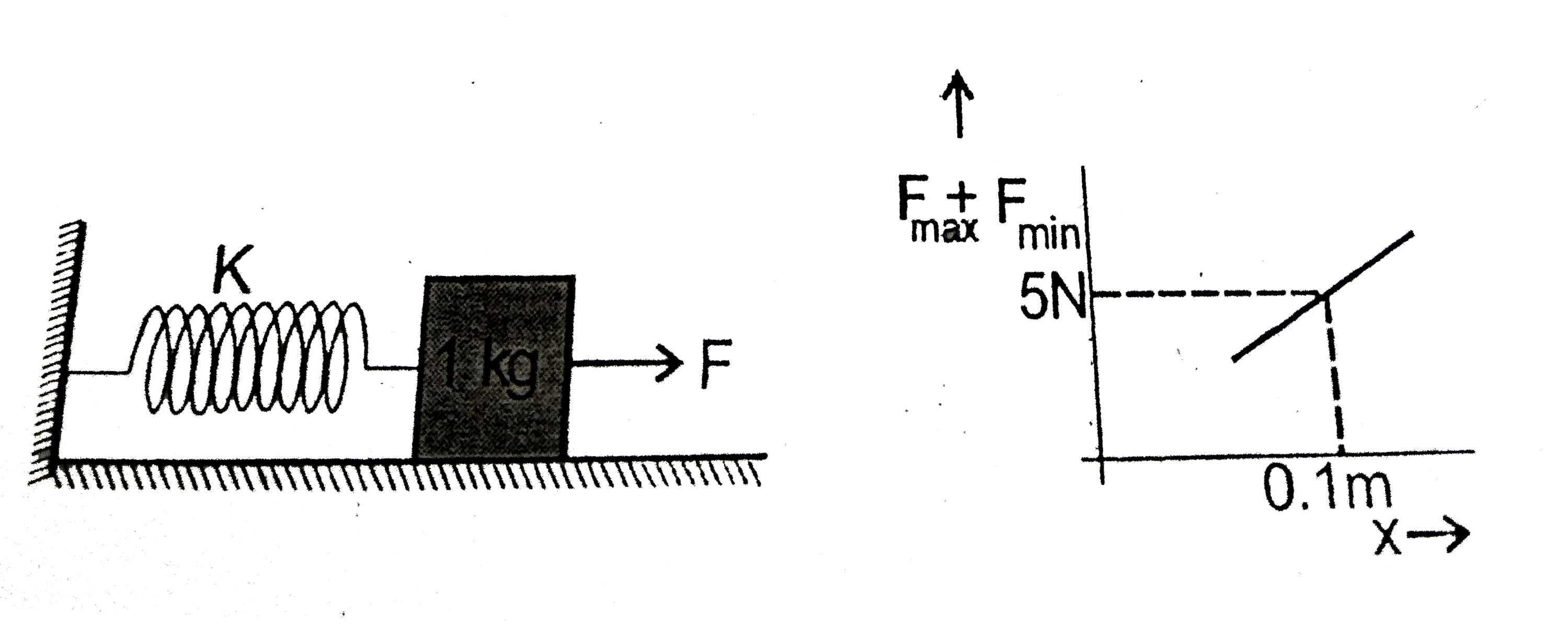
The spring constant of the spring is :
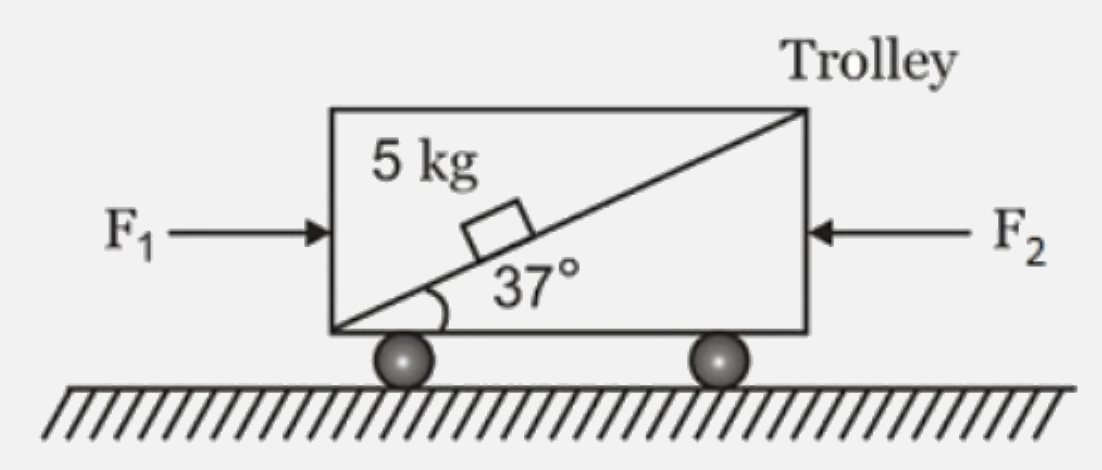
View SolutionThere is a trolley in which there is a fixed inclined surface on which a smooth block of mass 5kg is placed. Two horizontal forces of magnitude F1andF2 are applied on the trolley as shown to keep the trolley at rest. The value of F1−F2 is :
(Assume there is no friction between the trolley and horizontal ground and g=10ms−2)
View Solution
