In the figure shown, a force F is applied at the top of a disc of mass 4 kg and radius 0.25 m. find maximum velue of F for no slipping.

Till pure rolling continues we can fin α about bottommost point. About bottommost point torque of friction is zero.
α=F(2R)3/2mR2=4F3mR
a=Rα=4F3m
F+fmax=ma=4F3
F=3fmax=ma=4F3
F=3fmax=3μmg
=3×0.6×4×10=72N
This is the maximum value of applied force, as we have taken the maximum friction.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.11
Explore 2 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Assertion And Reason
Explore 11 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.9
Explore 2 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check

A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.Aa. Acceleration of disc = 2F/3mBb. Friction force between disc and surface = 2F/3Cc. Acceleration of disc = 6F/5mDd. Friction force between disc and surface is F/3
A constant force F is applied at the top of a ring as shown in figure. Mass of the ring is M and radius is R. Angular momentum of particle about point of contact at time t

View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View Solution
A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
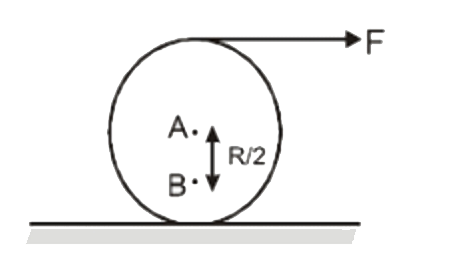
View SolutionA disc of mass m and radius R, is placed on a smooth text service fixed surface . Point A is the geometrical centre of the disc while point B is the centre of mass of the disc . The moment of inertia of the dics about an axis through its centre of mass and perpendicular to the plane of the figure is I .A constant force F is applied to the top of the disc . The acceleration of the centre A of the disc at the instant B is below A (on the same vertical line ) will be :
View SolutionA homogeneous block rests against a vertical wall for which the coefficient of friction is 1/2. A force 'F' is applied to the block in the direction as shown in figure. Find the maximum magnitude of applied force 'F' such that block remains in rest.

View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
View Solution