Block m is released from rest when spring is in its natural length ( assume pulley is ideal and block does not strike on ground during it's motion in vertical plane )
than :
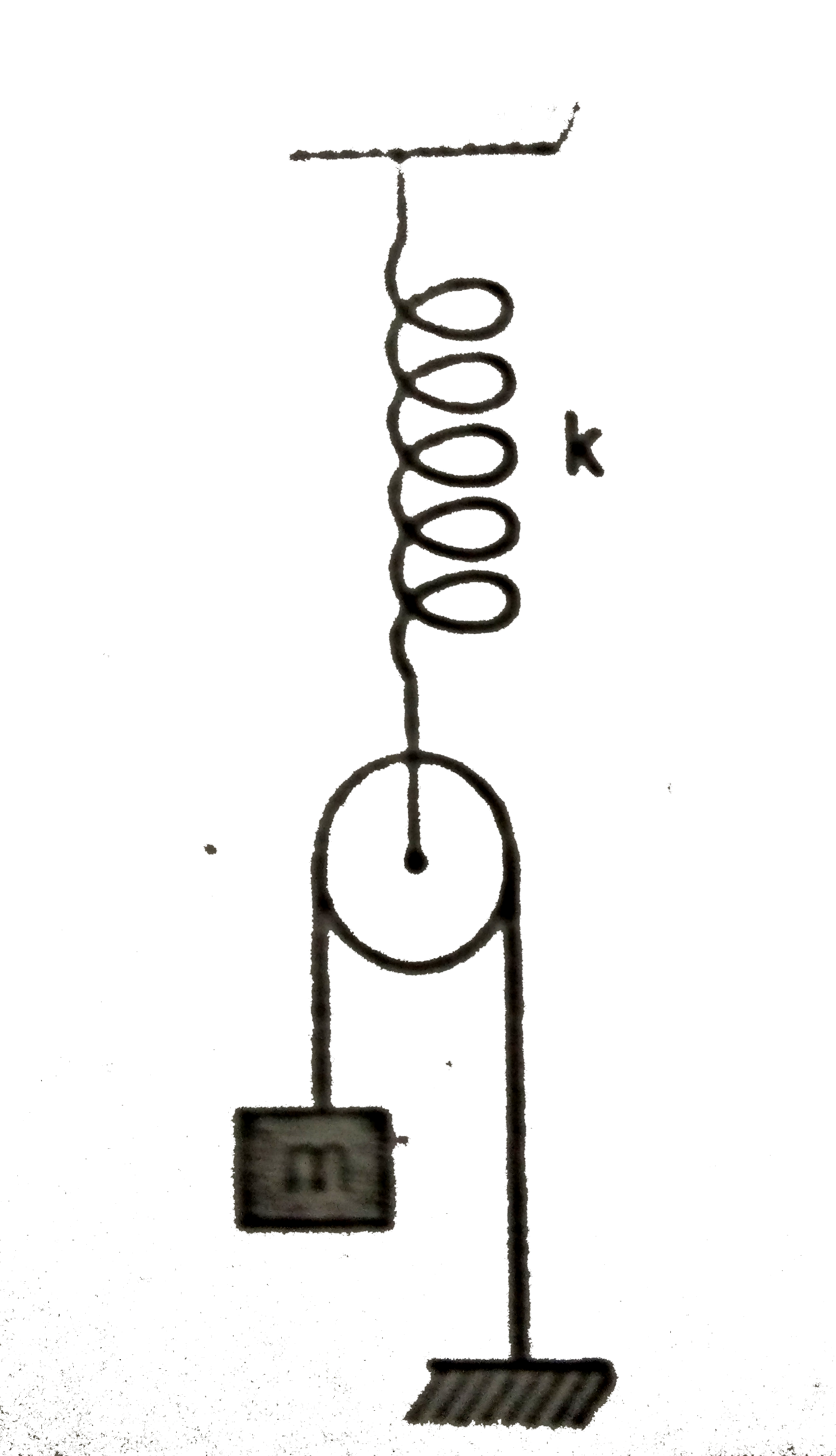
maximum elongation in spring is 4mg/k
maximum elongation in spring is 2mg/k
maximum speed of block is 2g√mk
maximum speed of block is g√mk
The correct Answer is:A, C
By energy conservation 12kx2=mg(2x)
⇒x=4mgk( maximum elongation )
at equilibrium kx=2mg
⇒x=2mgk
So (K.E.)max=mg(2x)−12kx2
=2mg(2mgk)−12k(2mgk)2
12mv2max=2m2g2k
⇒vmax=2g√mk
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 41
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 42
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 39
3 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionIn the figure, block A is released from rest when the spring is its natural length for the block B of mass m to leave contact with the ground at some stage what should be the minimum mass of block A?
 .
.
View SolutionIn figure, block A is released from rest, when spring is at its natural unstretched length. For block B of mass M to leave contact with the ground at some stage, the minimum mass of A must be
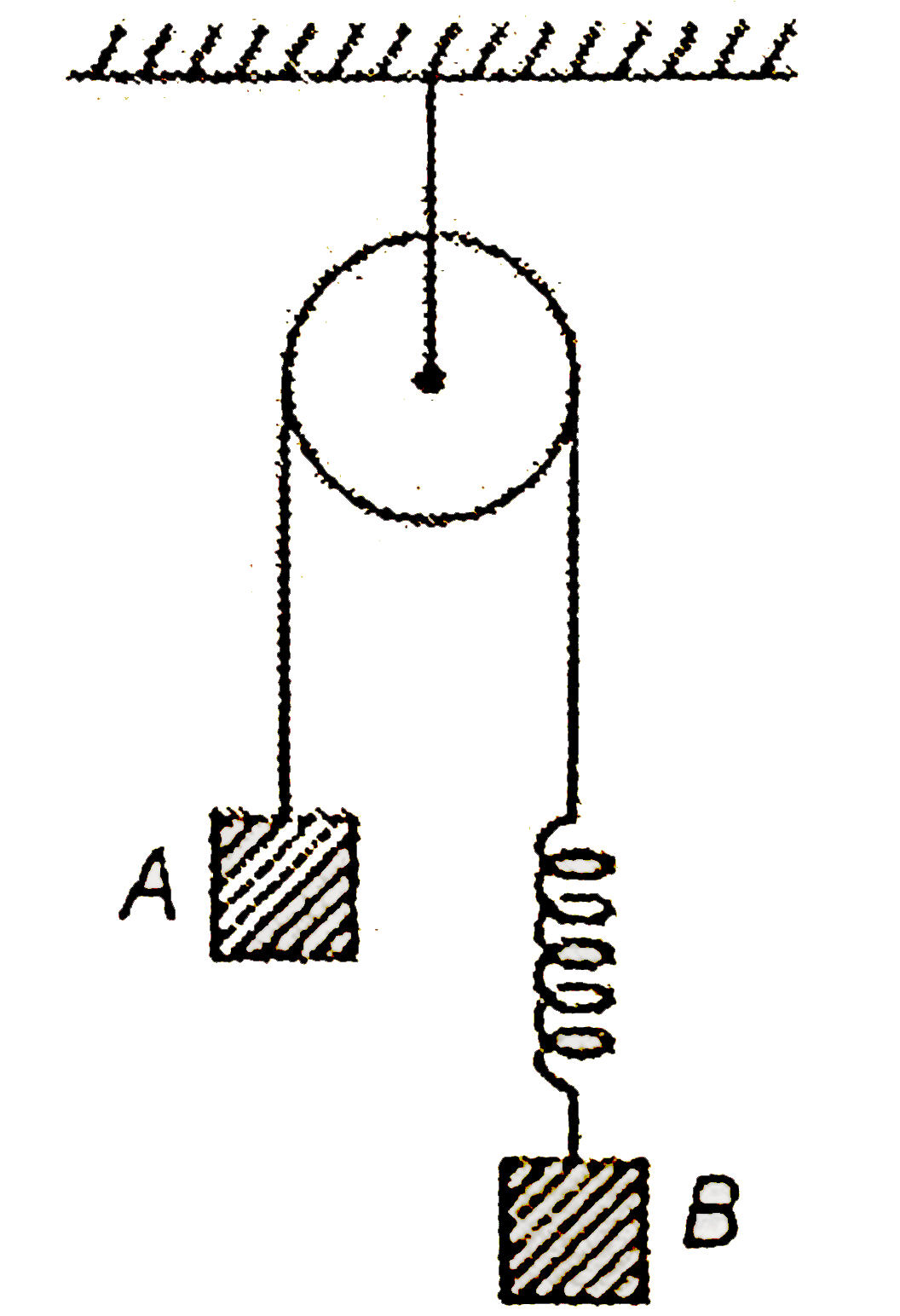
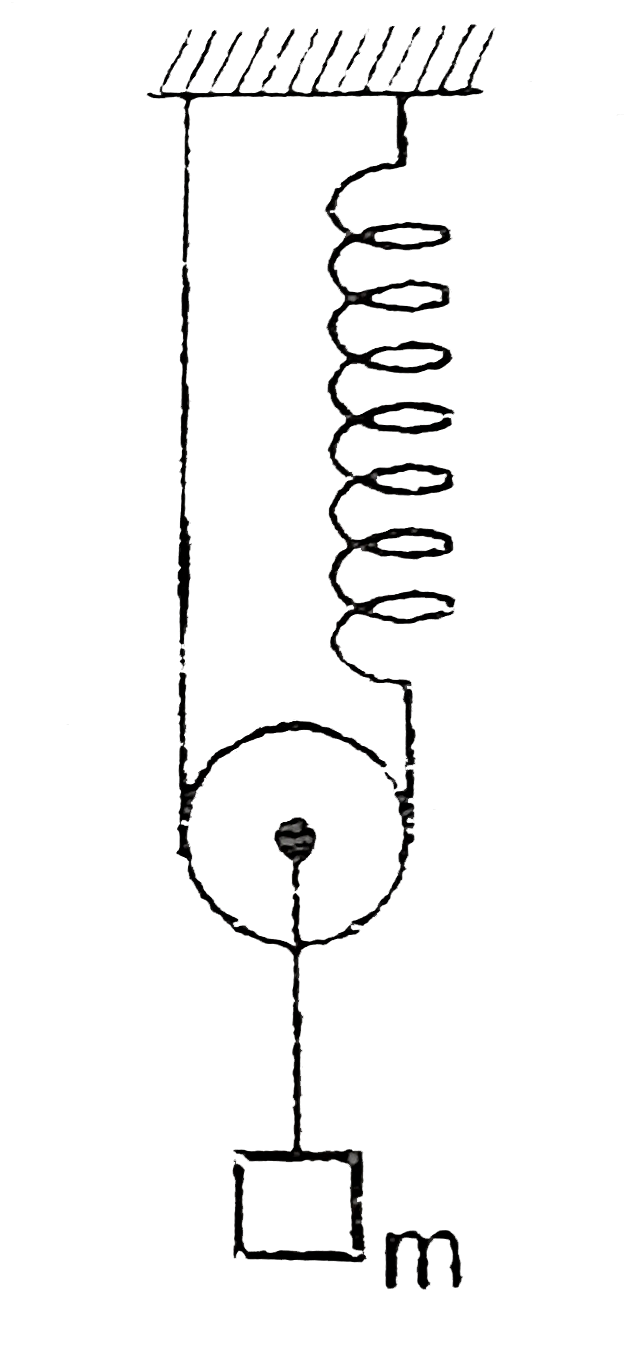
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionInitially spring is in natural length and both blocks are in rest condition. Then deter mine
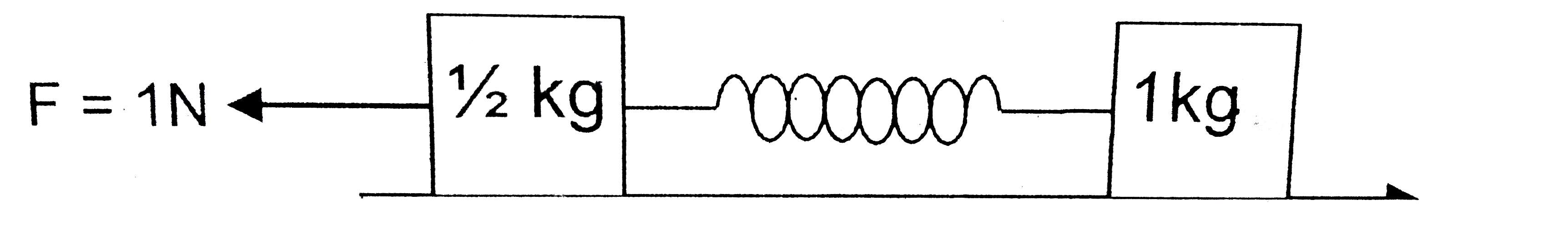
maximum extension in spring . K = 20 N/M
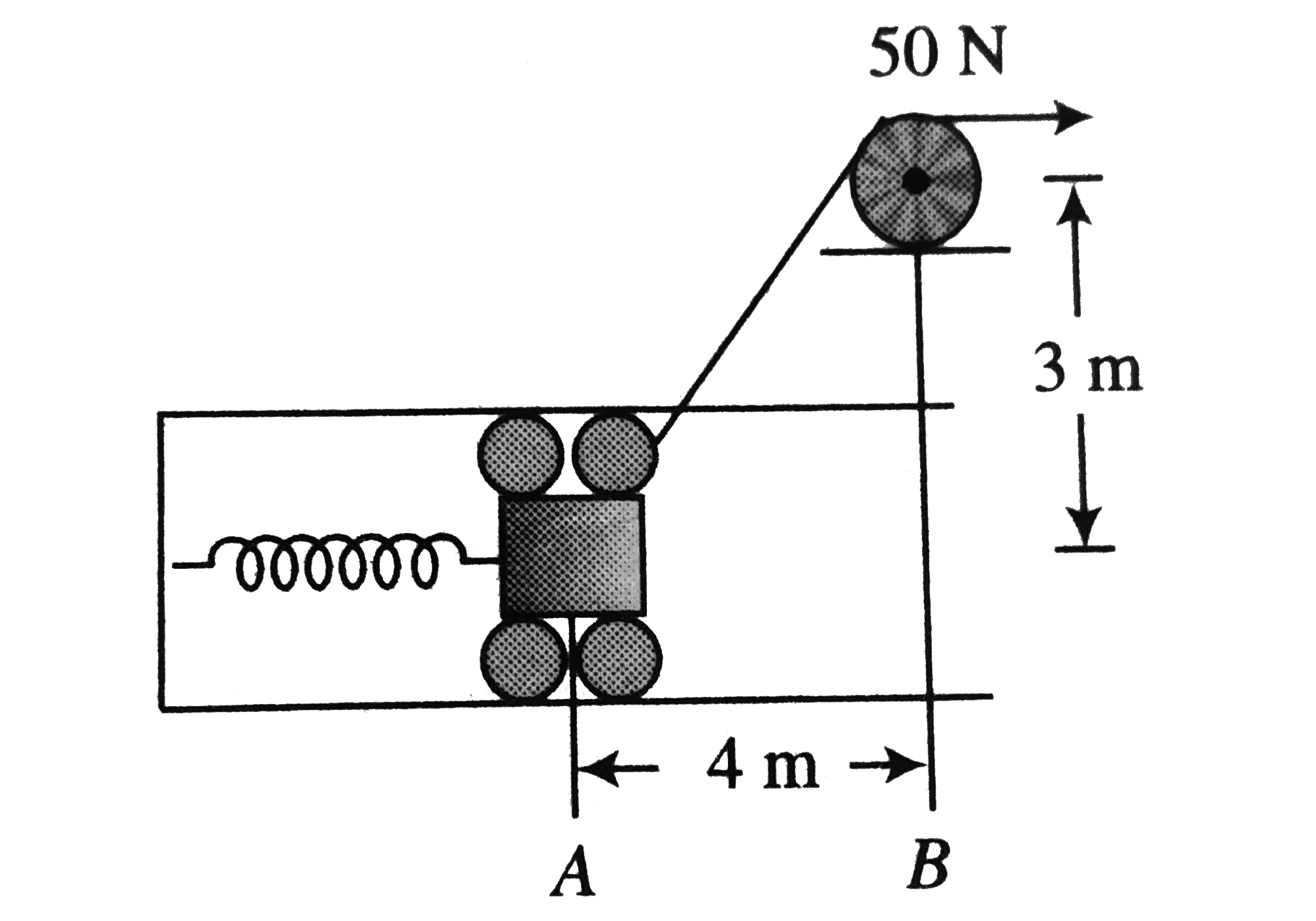
View SolutionA 20−kg block attached to a spring of spring constant 5Nm−1 is released from rest at A. The spring at this instant is having an elongation of 1m. The block is allowed to move in smooth horizontal slot with the help of a constant force 50N in the rope as shown. The velocity of the block as it reaches B is (assume the rope to be light)
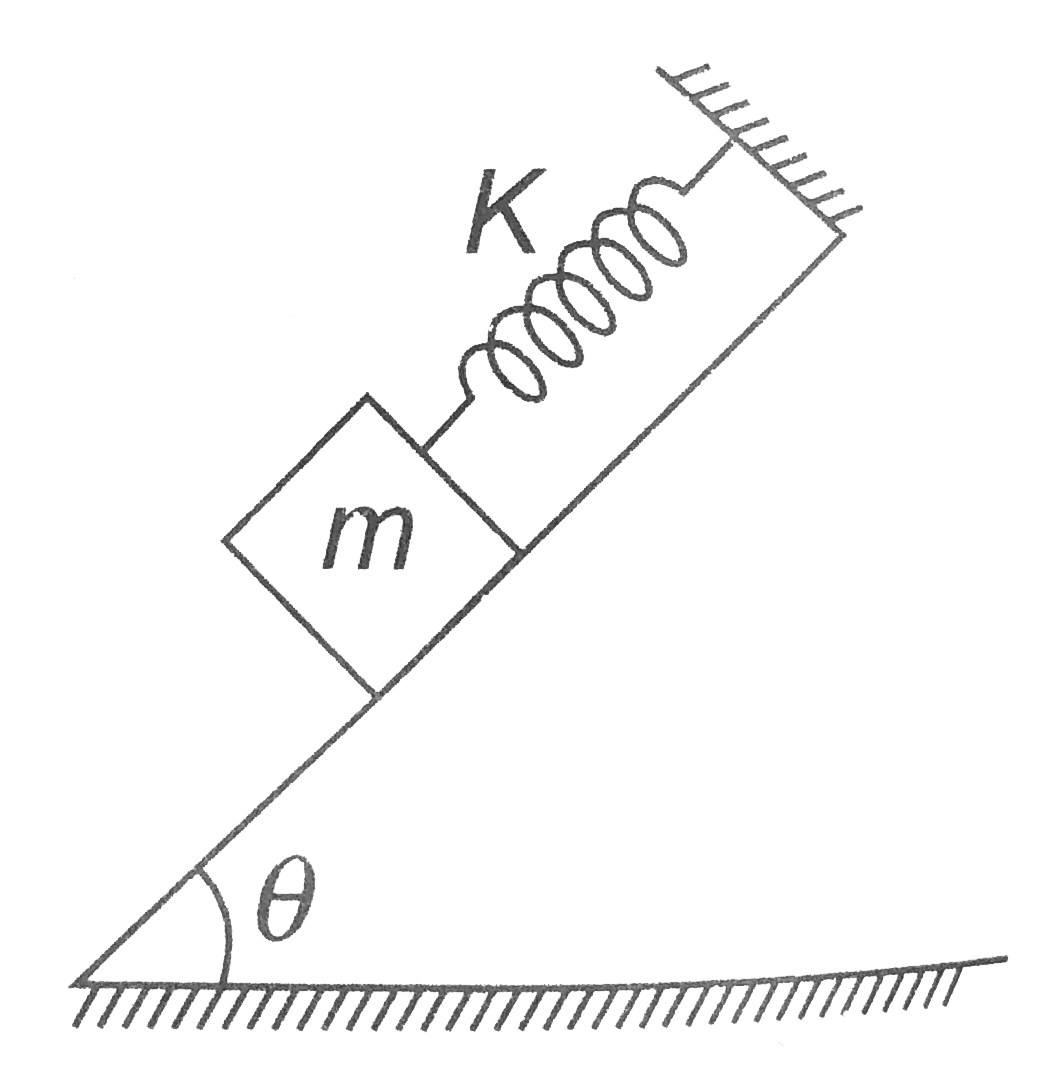
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
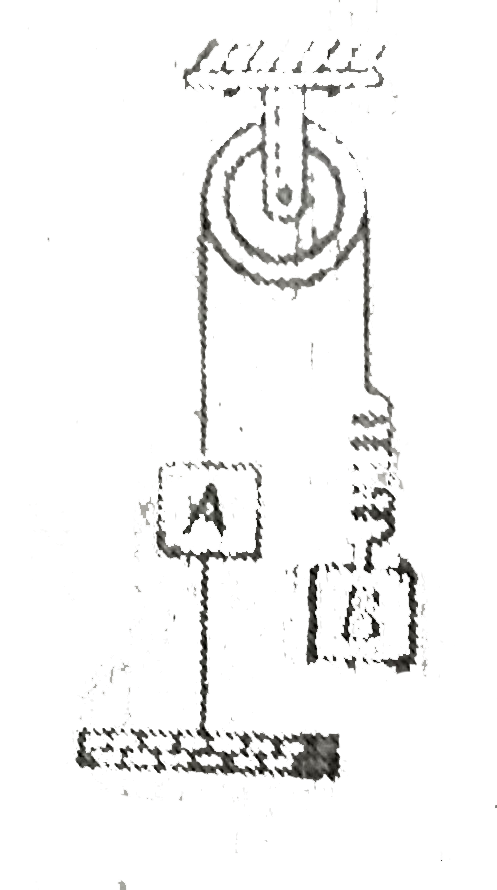
View Solution
