Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
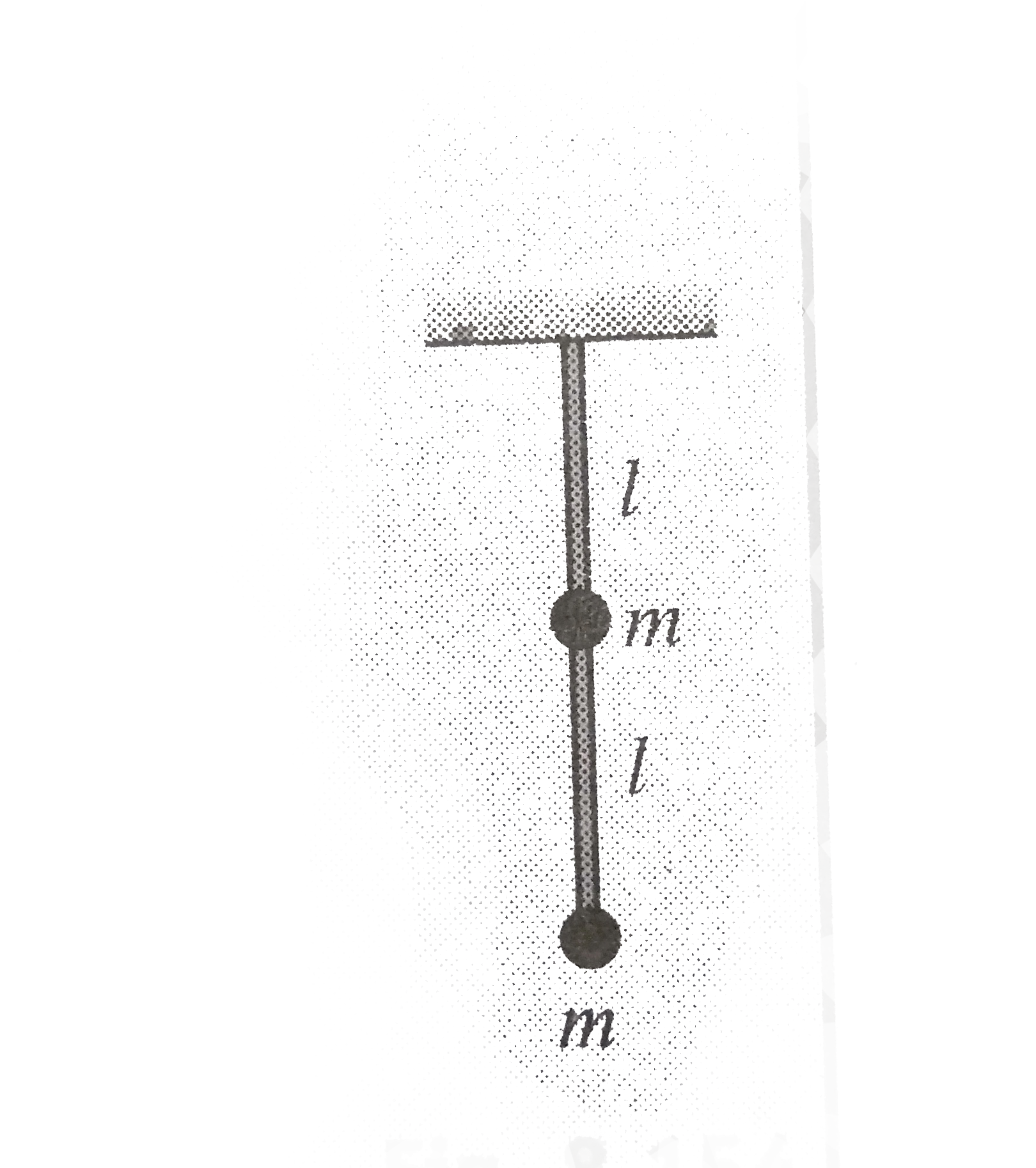
The correct Answer is:u=√485gl
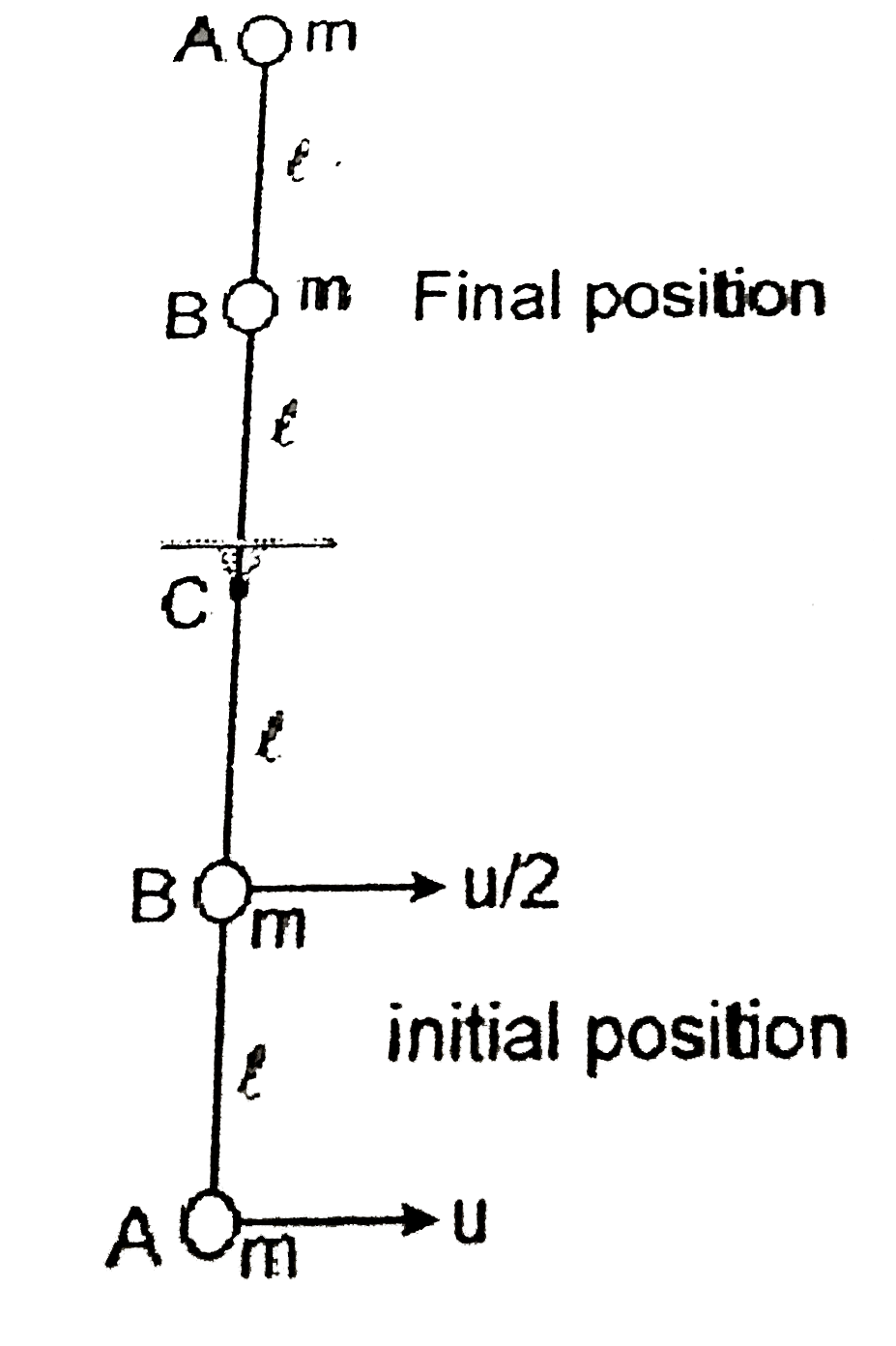
Let the initial given to the mass at A be u. Then the velocity of mass at B is u/2
As the system moves from initial the final position Increase in potential energy is 4ml+2mgl Decrease in kinetic energy.
=12mu2+12m(u2)2=52mu2
From conservation of energy
58mu2=6mloru=√485gl
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 445videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 457videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 427videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 View Solution
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 View Solution
View SolutionA mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
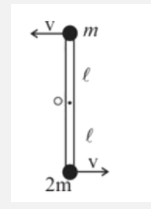 View Solution
View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
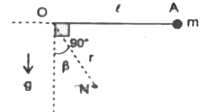 View Solution
View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
 View Solution
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView SolutionA rod of mass m and length l is connected with a light rod of length l. The composite rod is made to rotate with angular velocity ω as shown in the figure. Find the
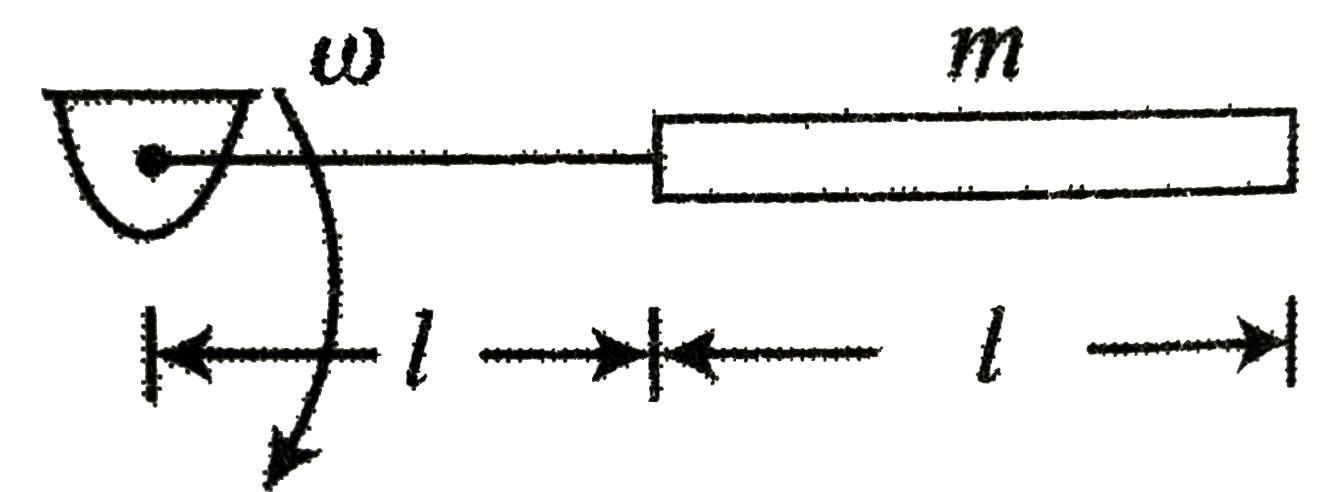
a. translational kinetic energy.
b. rotational kinetic energy.
c. total kinetic energy of rod.View Solution
A small ball of mass m hits the cylinder which is hinged at top and free to rotate in vertical plane as shown in figure. Mass of cylinder is M. Linear momentum of system (ball+cylinder)View SolutionTwo beads of mass 2m and m, connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure )

If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :View Solution

