A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
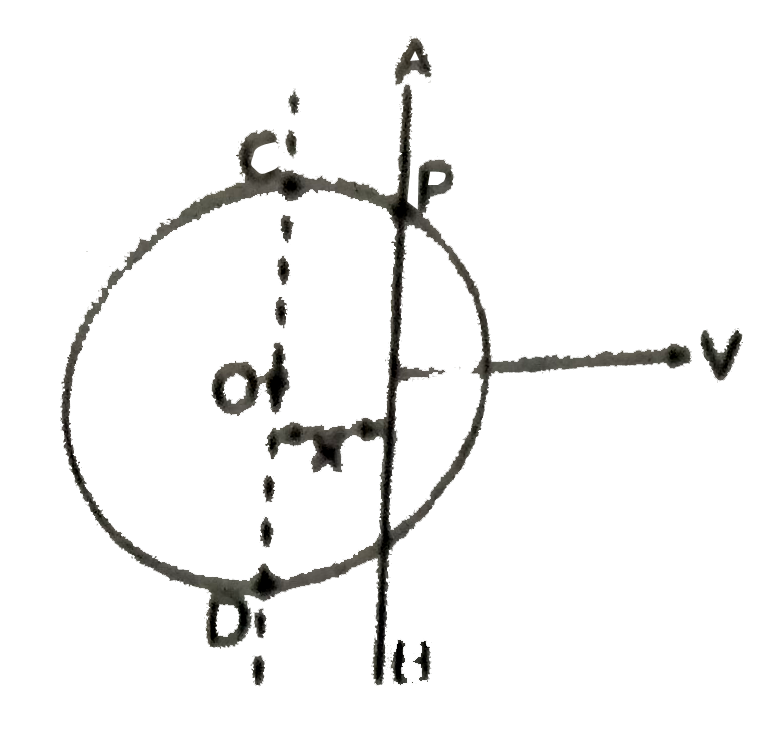
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
The correct Answer is:(a)p=54V(v)Vcosecθ
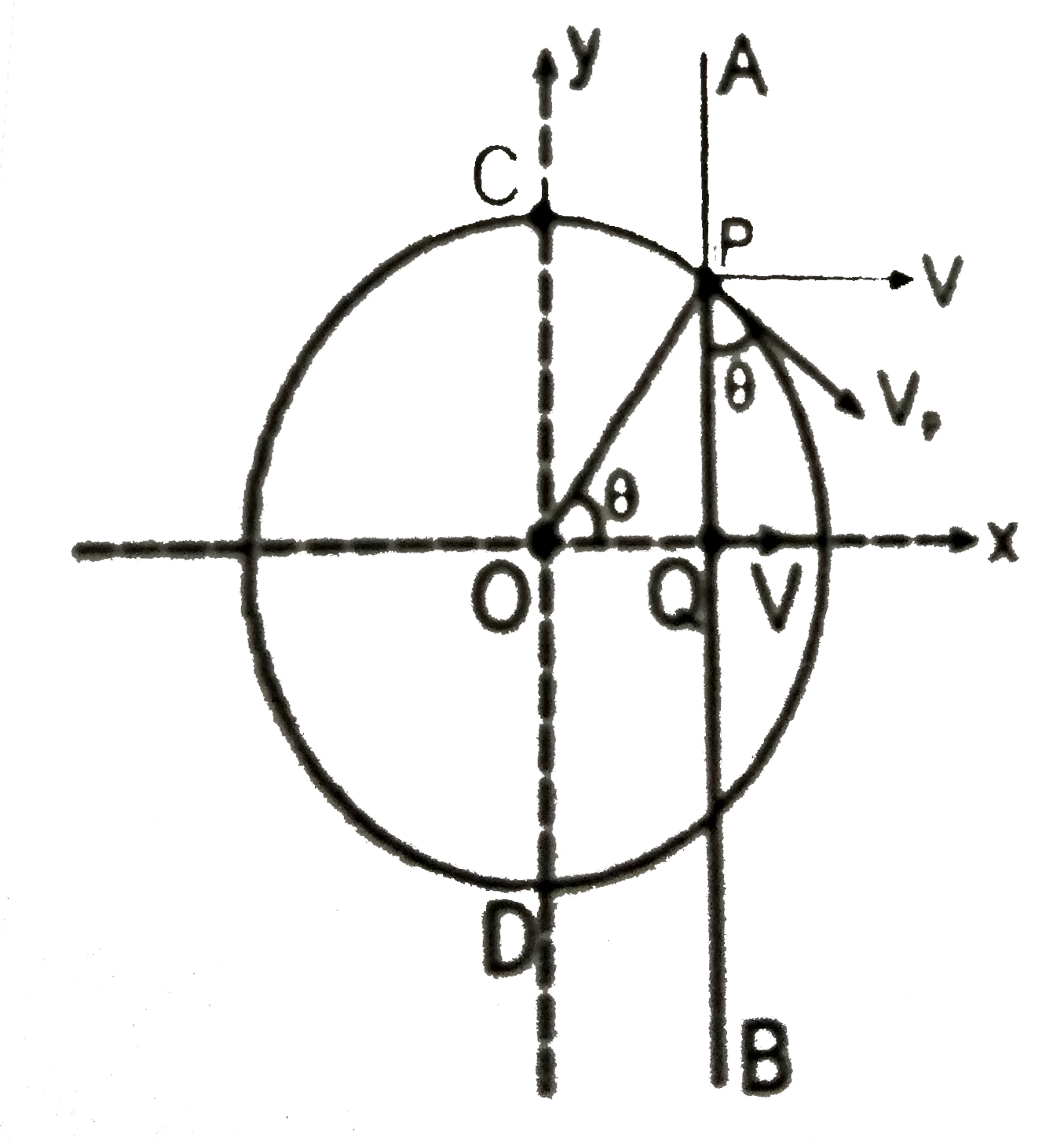
As a rod AB moves, the point 'P' will always lies on the circle.
∴Its velcoity will be along the circle as shown by 'VP' in the figure. If the point P has to lie on the rod 'AB' also then it should have component in 'x' direction as 'V'
∴VPsinθ=V
⇒Vp=Vcosecθ
herecosθ=xR=1R.3R5=35
....Ans.
ω=VPR=5V4R
ALTERNATE SOLUTION :
Sol. (a) Let 'P' have coordinate (x,y)
x=Rcosθ,y=Rsinθ
Vx=dxdt=−Rsinθdθdt=V⇒dθdt=−VRsinθ
Vy=Rcosθdθdt=Rcosθ(−VRsinθ)
=−Vcotθ
∴VP=√V2x+V2y=√V2+V2cot2θ
=Vcosecθ....Ans.
Sol.(b)ω=VPR=5V4R
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 64
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 65
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 62
4 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction. Separated by a distance r. Then the angular velocity of the rod is :
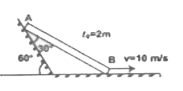
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

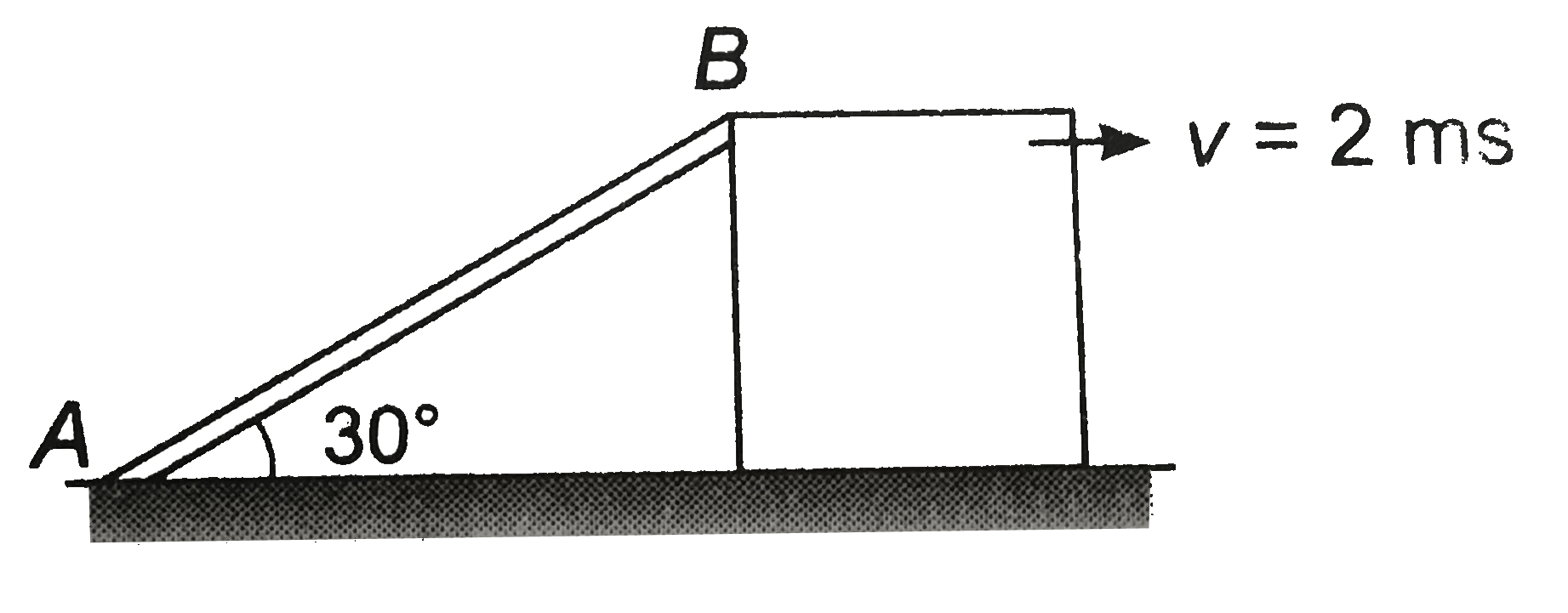
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
View SolutionThe velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

View SolutionA rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
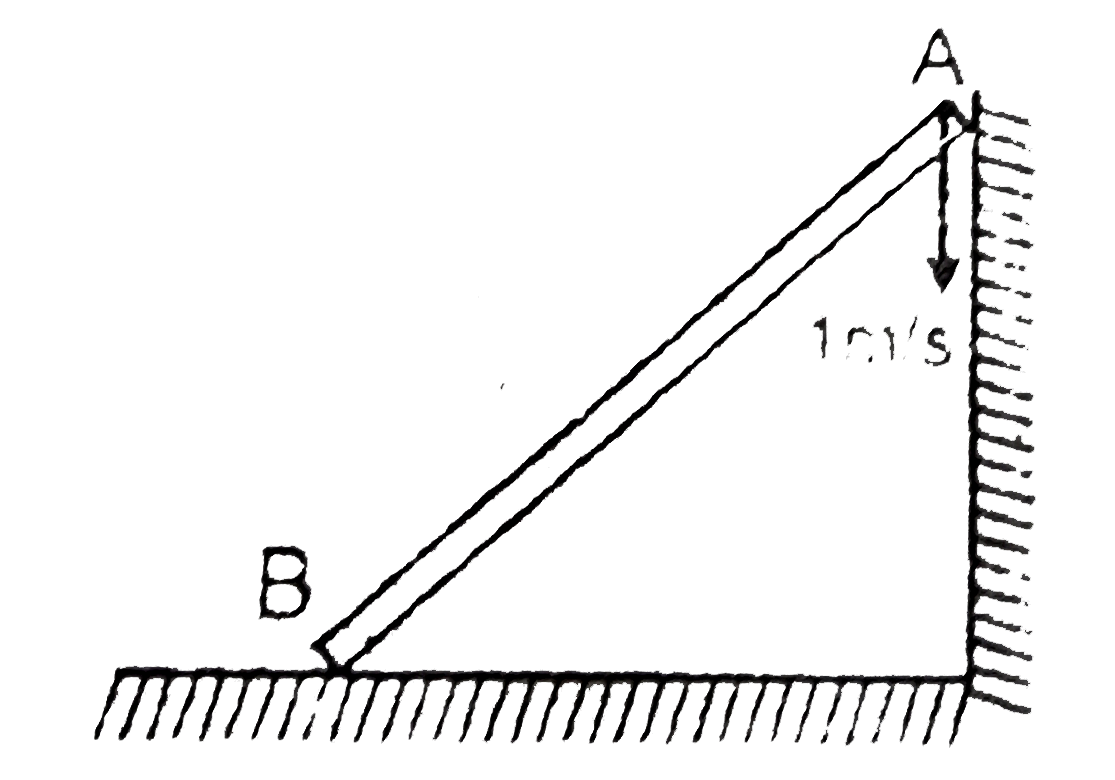
View SolutionFind the velocity of the moving rod at time t if the initial velocity of the rod is zero and a constant force F is applied on the rod.Neglect the resistance of the rod.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View SolutionIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be

View Solution
