Two points of a rod move with velocity and perpendicular to the rod and in the same direction. Separated by a distance . Then the angular velocity of the rod is :
The correct Answer is:D
is the velocity of one point w.r.t other perpendicular to rod.
and being the distance between the points
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
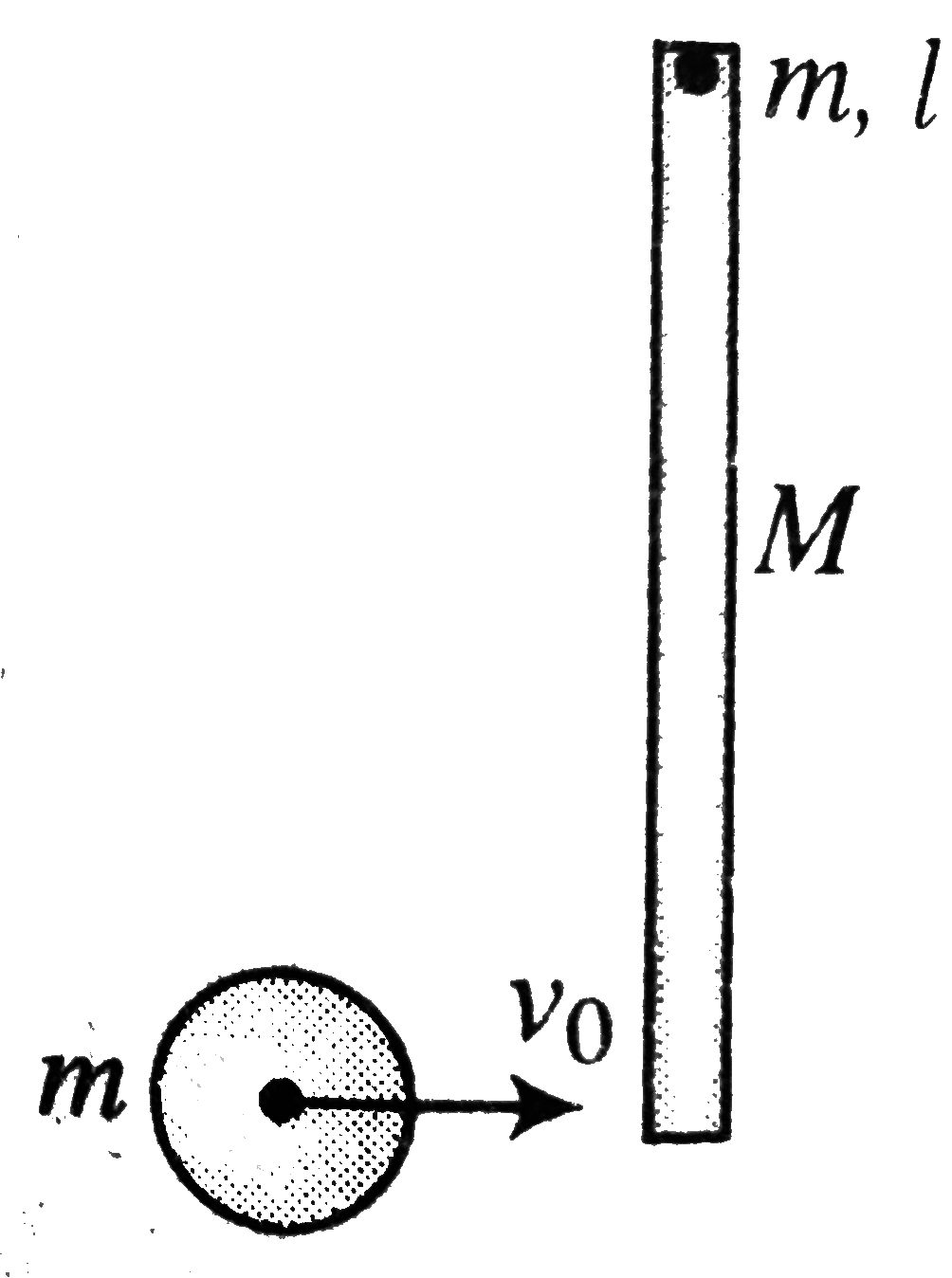
A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod of length 8 a and mass 6 m lies on a smooth horizontal surface. Two point masses m and 2 m moving in the same plane with speed 2 v and v respectively strike the rod perpendicular at distances a and 2a from the mid point of the rod in the opposite directions and stick to the rod. The angular velocity of the system immediately after the collision is
View SolutionA uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angulr velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View Solution
A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
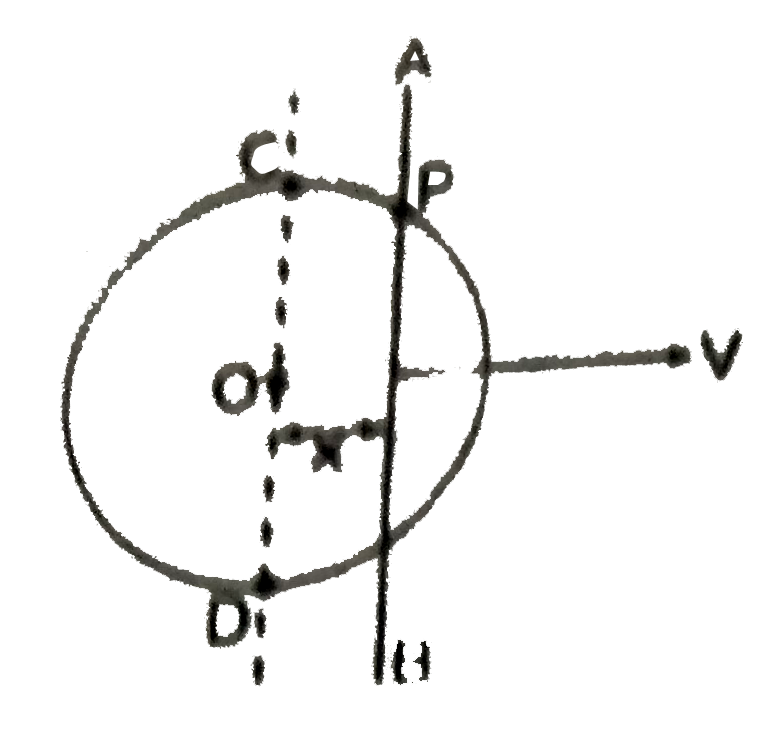
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
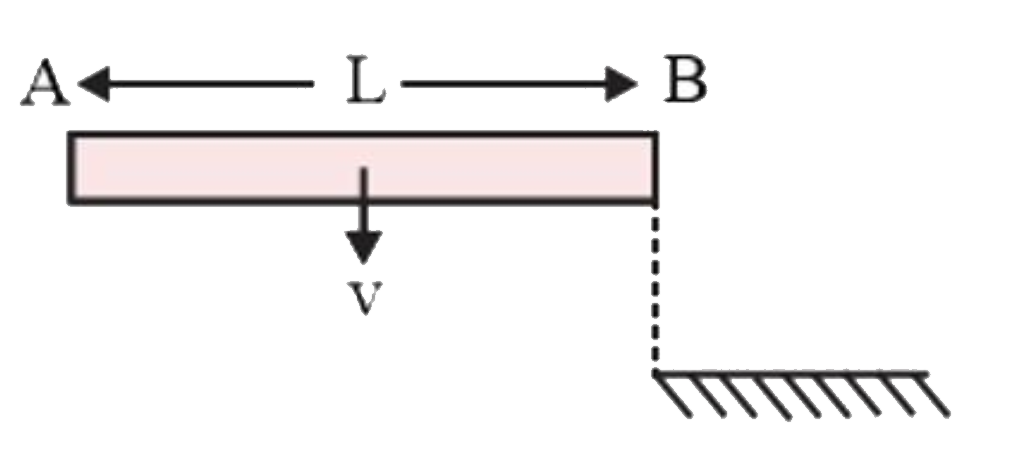
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
View SolutionA homogenous rod of length l=ηx and mass M is lying on a smooth horizontal floor. A bullet of mass m hits the rod at a distance x from the middle of the rod at a velocity v0 perpendicular to the rod and comes to rest after collision. If the velocity of the farther end of the rod just after the impact is in the opposite direction of v0, then:
View SolutionA rod of mass m and length l in placed on a smooth table. An another particle of same mass m strikes the rod with velocity v0 in a direction perpendicular to the rod at distance x(<l/2) from its centre . Particle sticks to the end. Let ω be the angular speed of system after collision , then
Find the maximum possible value of impulse (by varying x) that can be imparted to the particle during collision. Particle still sticks to the rod.
View Solution
