A ball tied to the end of the string swings in a verticla plane in a vertical circle under the influence of gravity.
When the string makes an angle 90∘ with the vertical, the tangential acceleration is zero and radial acceleration is somewhere between minimum and maximum.
When the string makes an angle 90∘ with the vertical , the tangential acceleration is maximum and radial acceleration is somewhere between maximum and minimum.
At no plae in circular motion, tangential acceleration is equal to radial acceleration ( in magnitude )
When radial acceleration has its maximum value, the tangential acceleration is zero.
The correct Answer is:B, D
Step by step video & image solution for A ball tied to the end of the string swings in a verticla plane in a vertical circle under the influence of gravity. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 78
3 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 79
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 76
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Arn where A is a constant, r is the instantaneous radius of the circle and n=....
View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
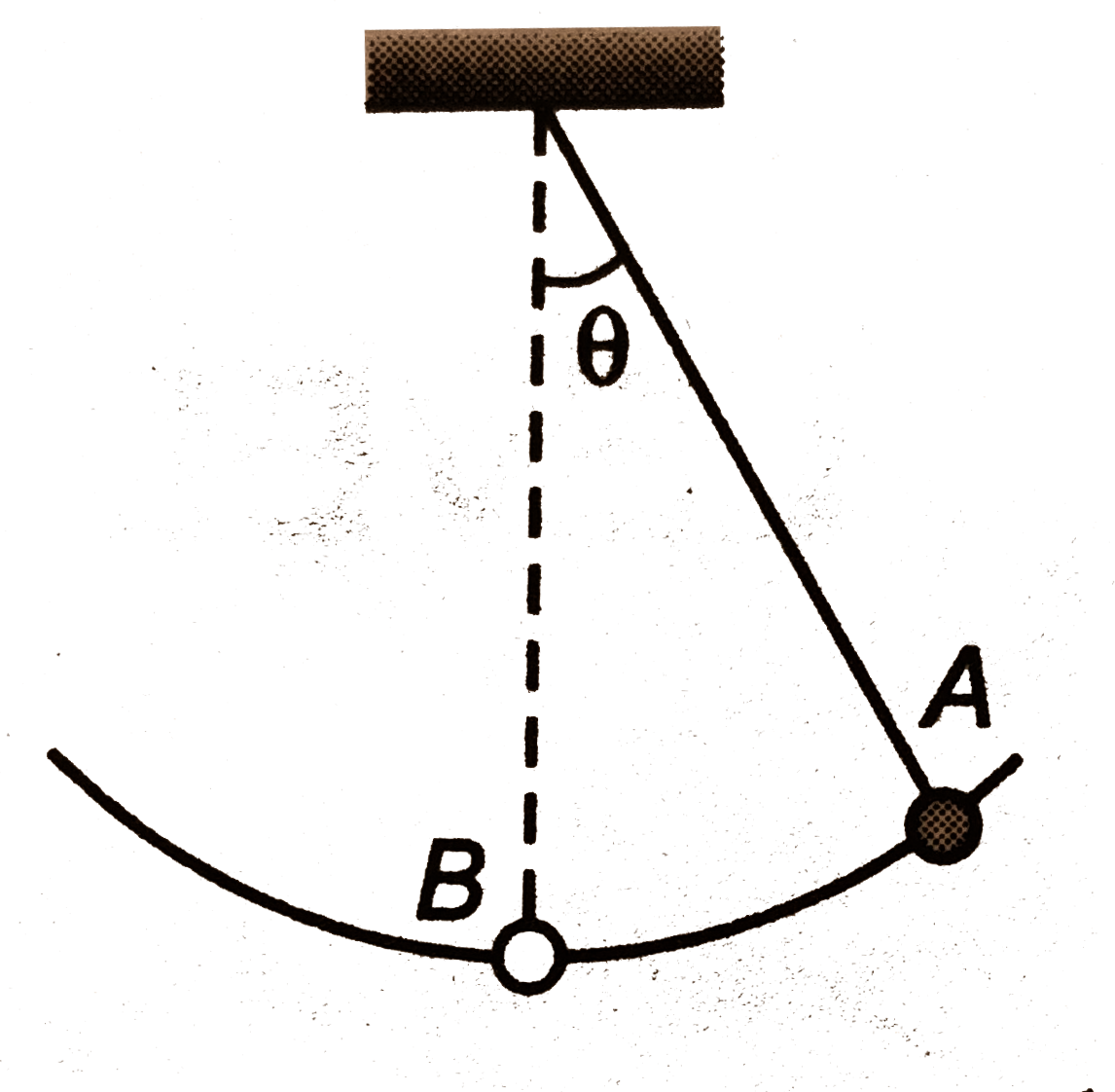
View Solution
Knowledge Check
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Arn where A is a constant, r is the instantaneous radius of the circle and n=....
Aa. -3Bb. 3Cc. 2Dd. -4
A massless, inextensible string of length 1 m has a breaking strength of 1 kg wt. A stone of mass 0.2 kg tied to one end of the string is made to move in a vertical circle. Can the stone describe the vertical circle? (g=10ms−2)
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
View SolutionA block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
View SolutionA stone of mass of 1 kg is tied to the end of a string 1 m long. It is whirled in a vertical circle. The velocity of the stone at the bottom of the circle is just sufficient to take it to the top of circle without slackening of the string. What is the tension in the string at the top of the circle? (Take, g =10 ms−2)
View SolutionA stone of mass 0.3 kg tied to the end of a string in a horizontal plane in whirled round in a circle of radius 1 m withp. speed of 40 rev/min. What is the tension in the string ? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N ?
View Solution
