The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
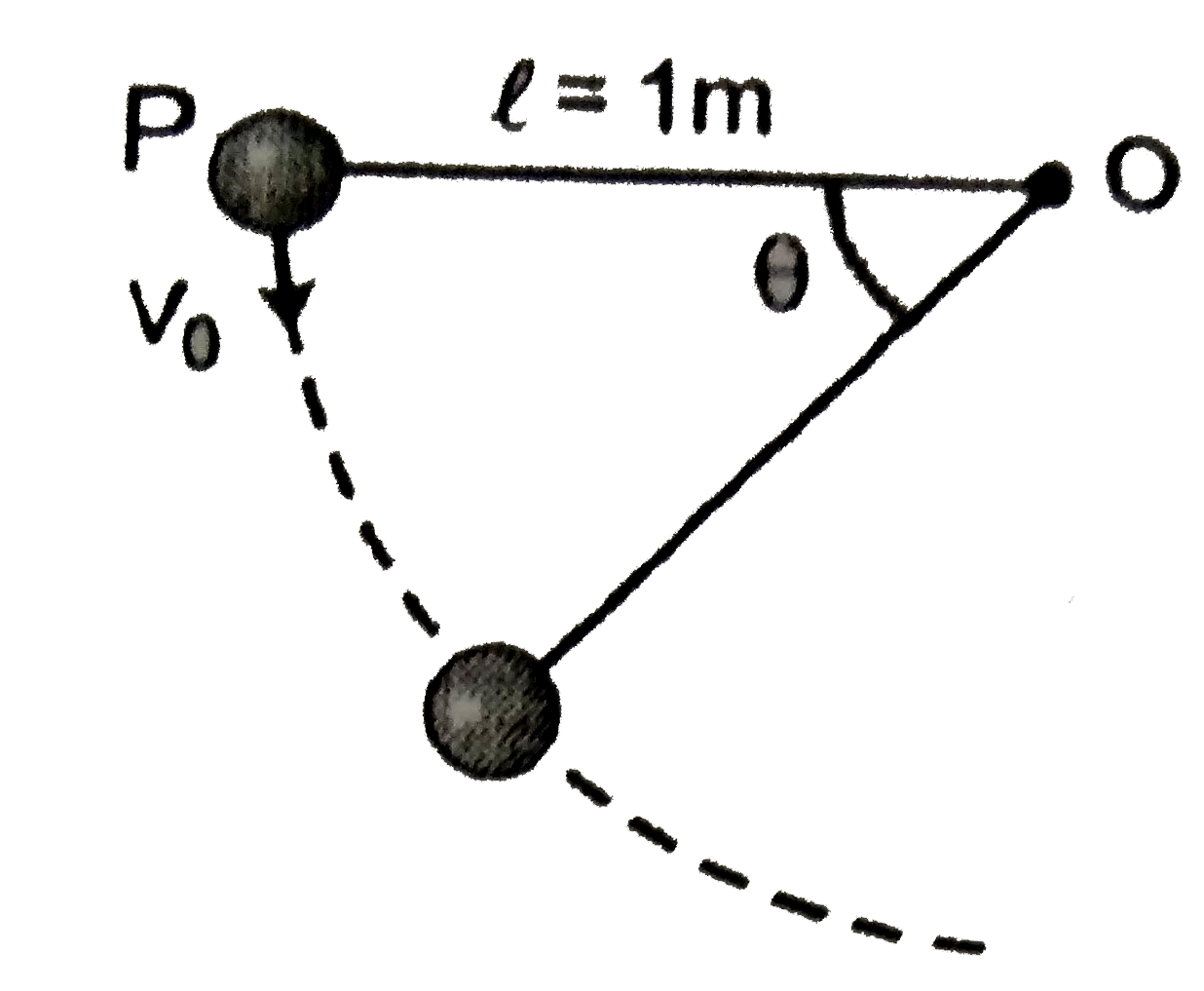
g2m/s
2g3m/s
√3g2m/s
will have minimum value 38m
The correct Answer is:C
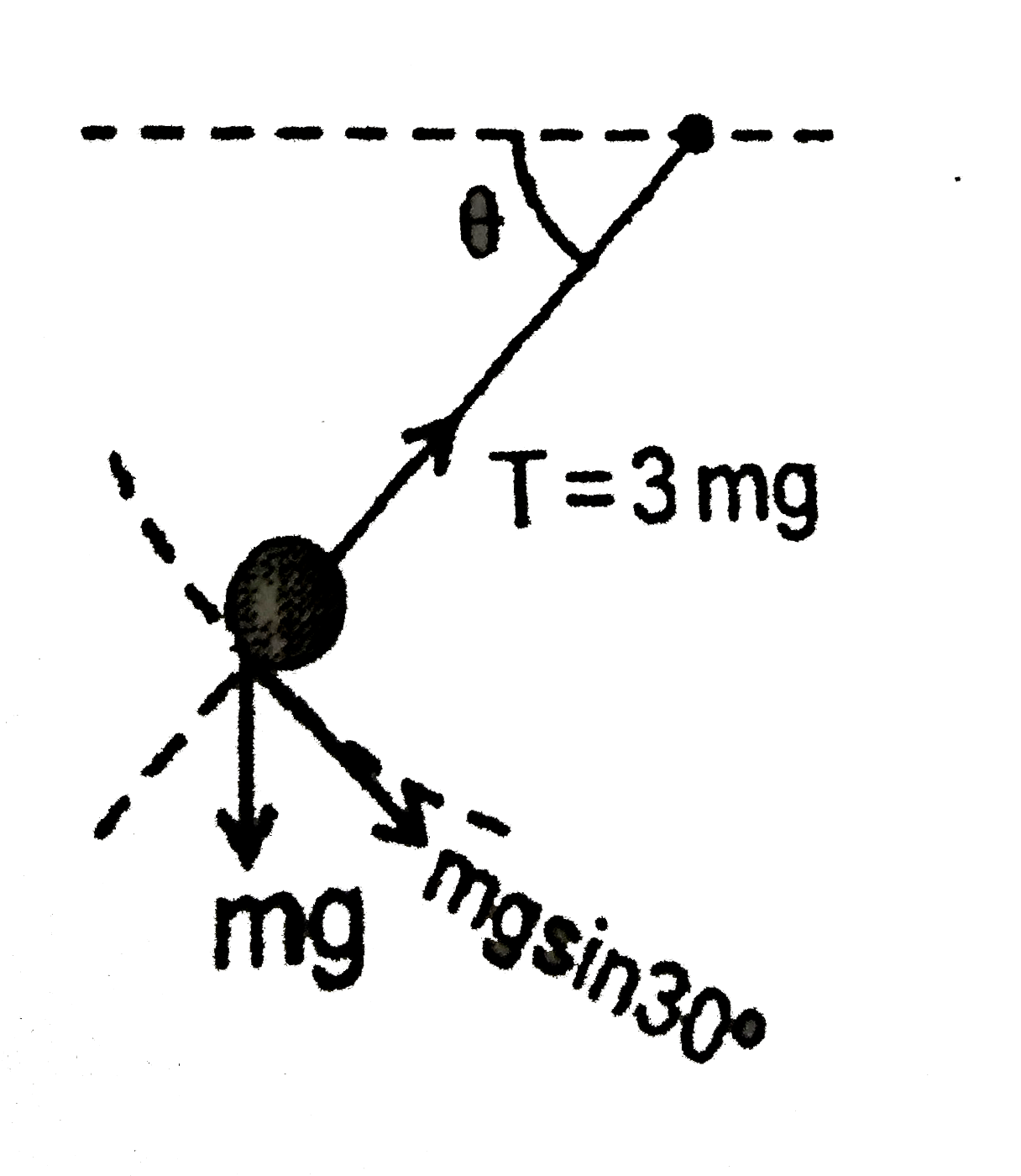
T=mgsinθ=mv2R
⇒3mg−mgsin30∘
=m.(u20+2glsin30∘)l
∴u0=√3g/2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 824videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 836videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 804videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
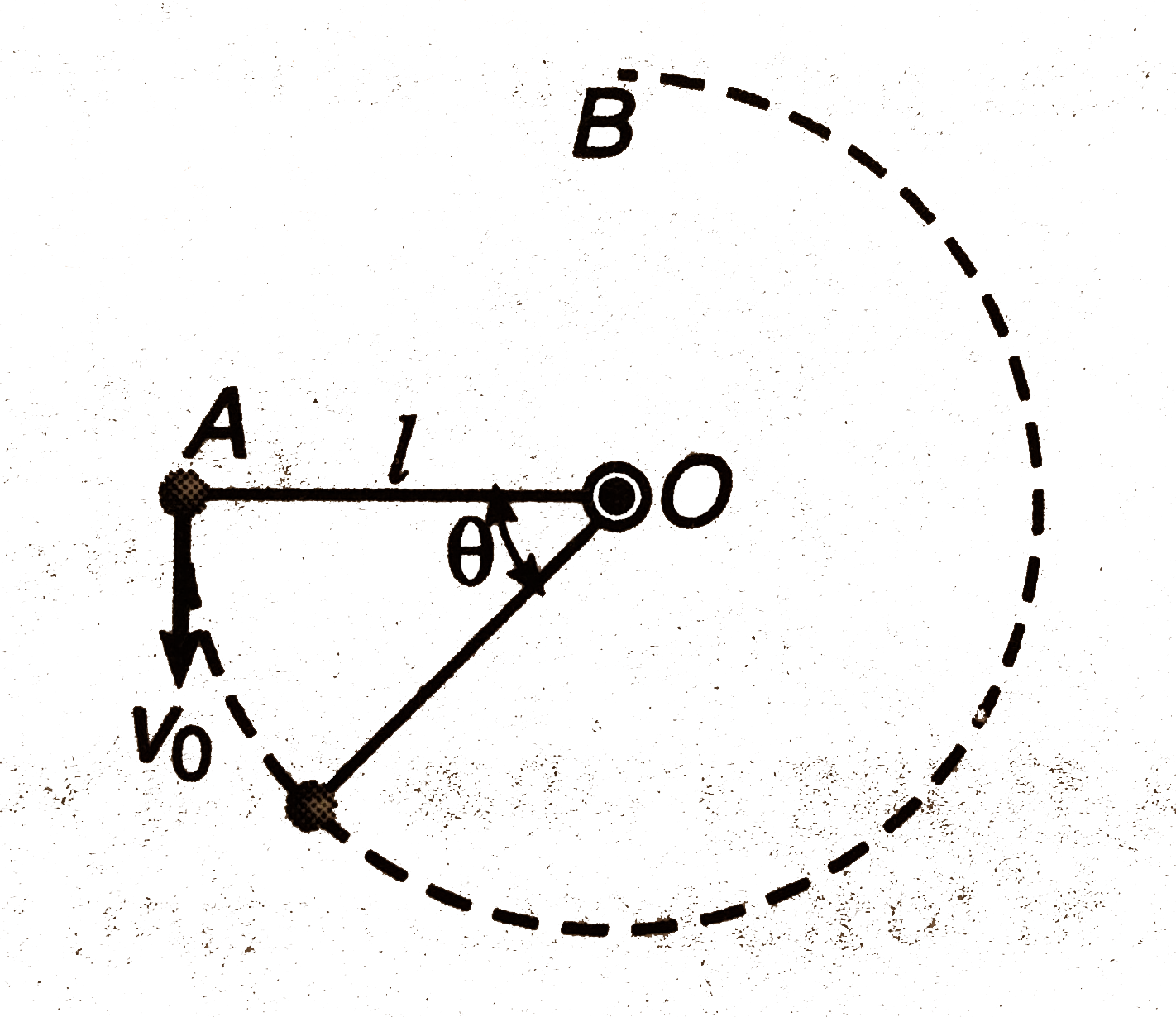 View Solution
View SolutionA small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A monkey of mass 40 kg climbs on a massless rope which can stand a maximum tension of 500 N. In which of the following cases will the rope break? (Take g=10ms−2)
 AThe monkey climbs up with an acceleration of 5ms−2.BThe monkey climbs down with an acceleration of 5ms−2.CThe monkey climbs up with a uniform speed 5ms−2.DThe monkey falls down, the rope freely under gravity.
AThe monkey climbs up with an acceleration of 5ms−2.BThe monkey climbs down with an acceleration of 5ms−2.CThe monkey climbs up with a uniform speed 5ms−2.DThe monkey falls down, the rope freely under gravity.
A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionA monkey A (mass = 5kg) is climbing up a rope tied to a rigid support. The monkey B (mass = 2kg) is holding on to the tail of monkey A. If the tail can tolerate a maximum tension of 30N, what force should monkey A apply on the rope in order to carry monkey B with it? (g=10m/s2).
View Solution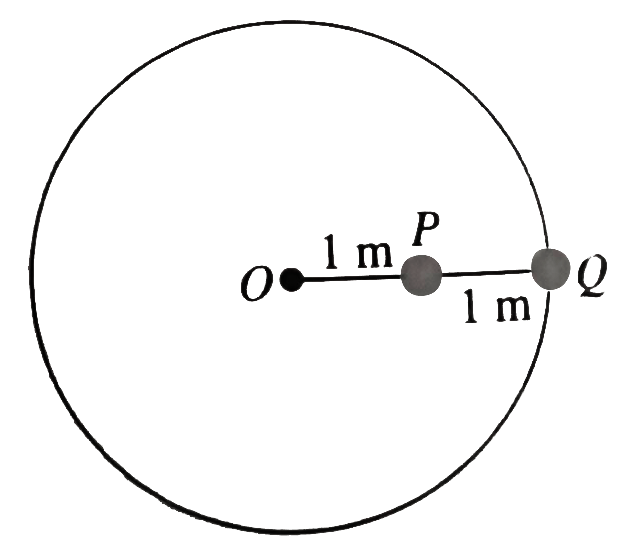
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio of their tension:View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View Solution

