A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
7.5 kg- m/s
15 kg - m/s
10 kg-m/s
20 kg-m/s
To find the change in linear momentum of a particle projected at an angle, we can follow these steps:
Step 1: Identify the Given Values
- Mass of the particle, m=1kg
- Initial velocity, v=40m/s
- Angle of projection, θ=30∘
- Acceleration due to gravity, g=10m/s2
- Time, t=1s
Step 2: Resolve the Initial Velocity into Components
The initial velocity can be resolved into horizontal (vx) and vertical (vy) components using trigonometric functions:
- vx=v⋅cos(θ)=40⋅cos(30∘)
- vy=v⋅sin(θ)=40⋅sin(30∘)
Calculating these:
- cos(30∘)=√32 and sin(30∘)=12
- vx=40⋅√32=20√3m/s
- vy=40⋅12=20m/s
Step 3: Calculate the Vertical Velocity after 1 Second
The vertical velocity after time t can be calculated using the equation:
vy,final=vy,initial−g⋅t
Substituting the values:
vy,final=20−10⋅1=10m/s
Step 4: Calculate the Change in Momentum
The change in momentum (ΔP) can be calculated using:
ΔP=m⋅(vy,final−vy,initial)
Substituting the known values:
ΔP=1⋅(10−20)=1⋅(−10)=−10kg m/s
Step 5: Conclusion
The change in linear momentum of the particle after 1 second is −10kg m/s.
---
- Mass of the particle, m=1kg
- Initial velocity, v=40m/s
- Angle of projection, θ=30∘
- Acceleration due to gravity, g=10m/s2
- Time, t=1s
The initial velocity can be resolved into horizontal (vx) and vertical (vy) components using trigonometric functions:
- vx=v⋅cos(θ)=40⋅cos(30∘)
- vy=v⋅sin(θ)=40⋅sin(30∘)
- cos(30∘)=√32 and sin(30∘)=12
- vx=40⋅√32=20√3m/s
- vy=40⋅12=20m/s
The vertical velocity after time t can be calculated using the equation:
vy,final=vy,initial−g⋅t
Substituting the values:
vy,final=20−10⋅1=10m/s
The change in momentum (ΔP) can be calculated using:
ΔP=m⋅(vy,final−vy,initial)
Substituting the known values:
ΔP=1⋅(10−20)=1⋅(−10)=−10kg m/s
The change in linear momentum of the particle after 1 second is −10kg m/s.
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Only one option is correct for JEE Advanced
60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct
1 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA particle of mass m is projected with a velocity v at an angle of θ with horizontal. The angular momentum of the particle at the highest point of its trajectory is equal to :
View SolutionA body is projected at angle 30° to horizontal with a velocity 50 ms−1 . Its time of flight is (g=10 m/s2)
View SolutionA body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionAn object of mass 10 kg is projected from ground with speed 40 m/s at an angle 60∘ with horizontal the rate of change of momentum of object one second after projection in SI unit is
[ Take g = 9.8 m/s2 ]
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA particle is projected at an angle of 30∘w.r.t. horizontal with speed 20m/s:( use g=10m/s2)
(i) Find the position vector of the particle after 1s.
(ii) Find the angle between velocity vector and position vector at t=1s.
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
Angular velocity of rod after collision is
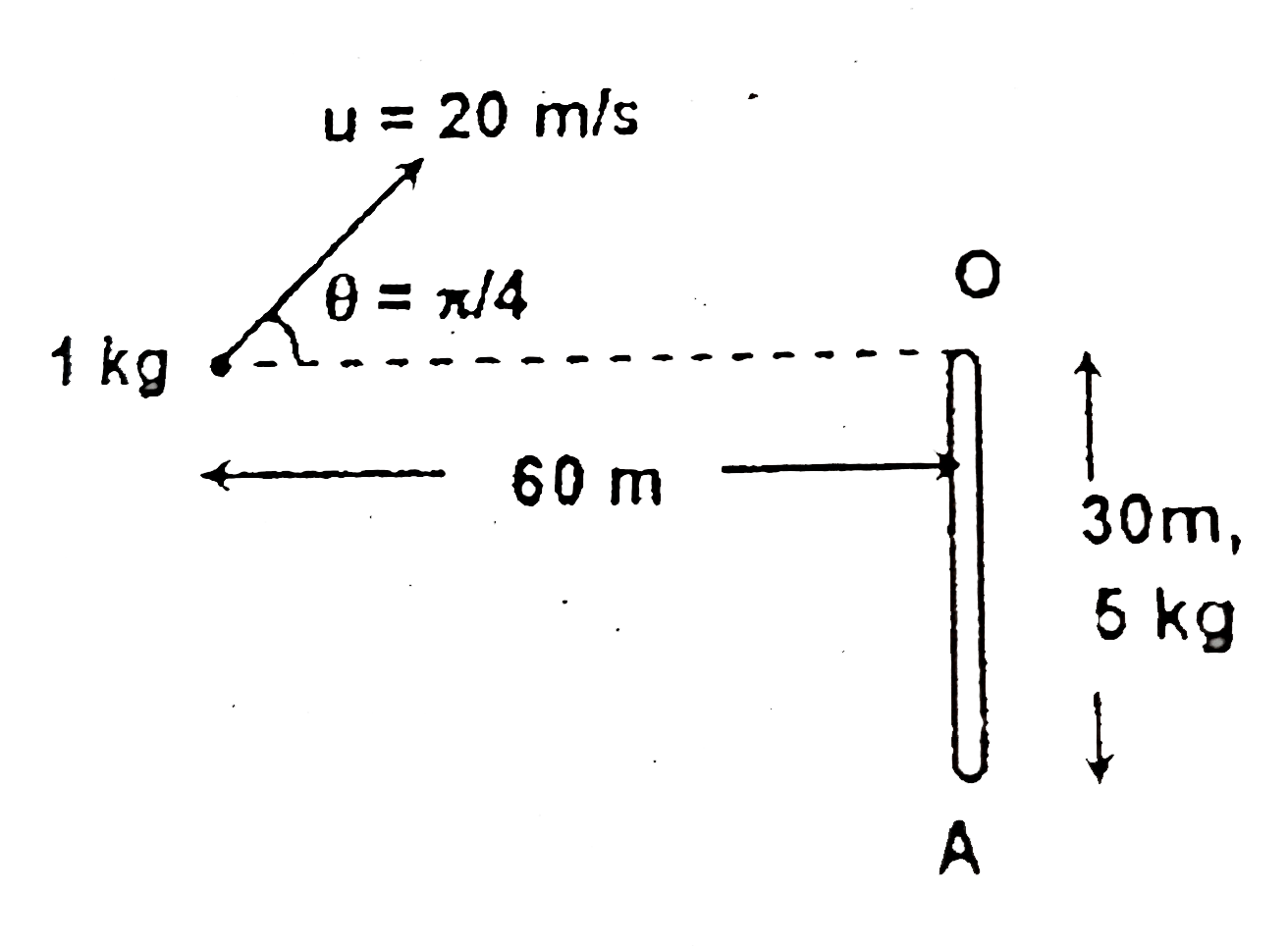
View Solution
