A string of length 'l' is fixed at both ends. It is vibrating in tis 3rd overtone with maximum amplitude 'a' the amplitude at a distance l3 from one end is
a
0
√3a2
a2
The correct Answer is:C
For a string vibrating in its nth overtong ((n+1)th harmonic)
y=2Asin((n+1)πxL)cosωt
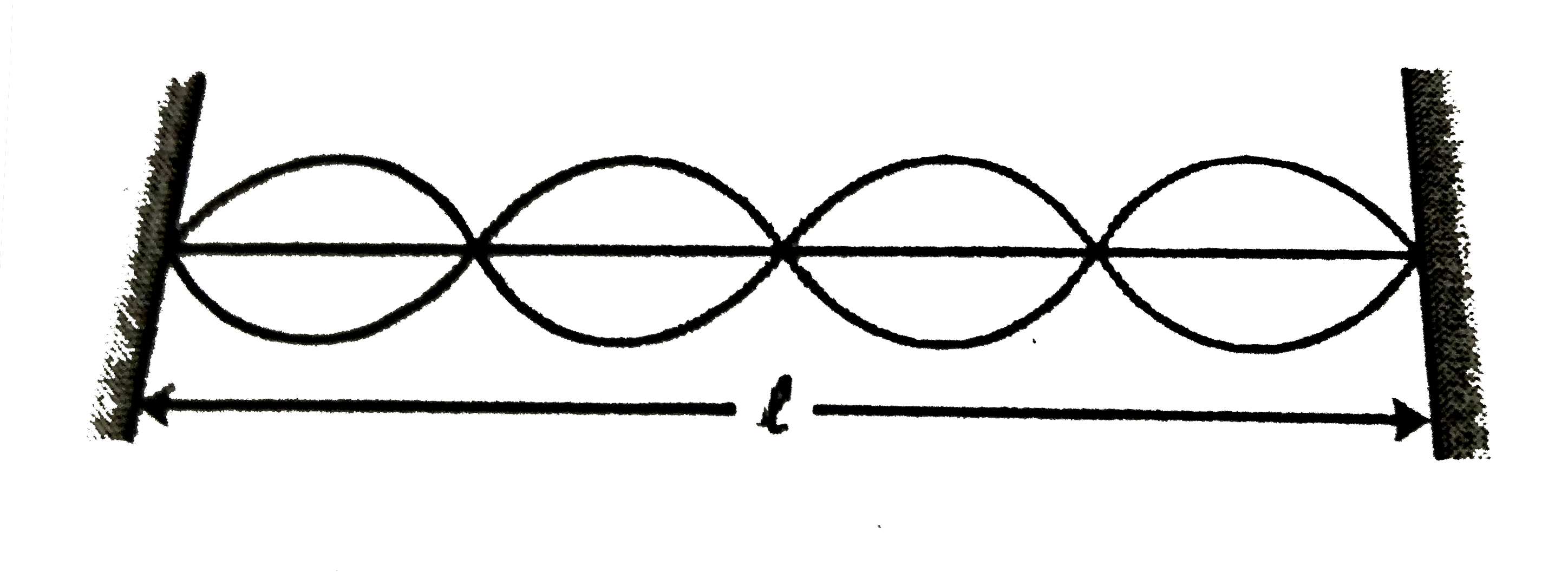
For x=l3,2A=a and n=3,
y=[asin(4πl.l3)]cosωt
=a.sin(4π3)cosωt
=−a.(√32)cosωt
i.e. at x=l3, the amplitude is √3a2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 86
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 87
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 84
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A string of length 'L' is fixed at both ends . It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance L/3 from one end is
View SolutionA closed organ pipe has length L. The air in it is vibrating in third overtone with maximum amplitude a . The amplitude at distanceL7 from closed of the pipe is a) 0 b) a c) a/2 d) data insufficient
View Solution
Knowledge Check
A string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz, then the waves would travel on its with a velocity of
A125 ms−1B250 ms−1C500 ms−1D1000 ms−1A streteched string of length l fixed at both ends can sustain stationary waves of wavelength λ given by
Aλ=n2/2lBλ=l2/2nCλ=2l/nDλ=2ln
A string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 5 mm. The amplitude of a particle at distance l/8 from the fixed end is
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA close organ pipe of diameter 10 cm has length 42 cm. the air column in pipe vibrates in its second overtone with the maximum amplitude ΔPo. The pressure amplitude at middle of pipe is
View SolutionA closed organ pipe of length L is vibrating in its first overtone there is a point Q inside the pipe at a distance 7L/9 form the open end the ratio of pressure amplitude at Q to the maximum pressure amplitude in the pipe is
View SolutionA string of length L, fixed at its both ends is vibrating in its 1st overtone mode. Consider two elements of the string of the same small length at positions l1=0.2Landl2=0.45L from one end.
If K1andK2 are their respective maximum kinetic energies,then
View SolutionA string fixed at both ends is vibrating in the lowest mode of vibration for which a point at quarter of its length from one end is a point of maximum vibration . The note emitted has a frequency of 100Hz. What will be the frequency emitted when it vibrates in the next mode such that this point is again a point of maximum vibratin ?
View Solution