A closed organ pipe of length L is vibrating in its first overtone there is a point Q inside the pipe at a distance 7L/9 form the open end the ratio of pressure amplitude at Q to the maximum pressure amplitude in the pipe is
1:2
2:1
1:1
2:3
The correct Answer is:A
To solve the problem, we need to find the ratio of the pressure amplitude at point Q (located at a distance of 7L9 from the open end) to the maximum pressure amplitude in a closed organ pipe vibrating in its first overtone.
1. Understand the Closed Organ Pipe:
- A closed organ pipe has one end closed and one end open. In the first overtone (which is the second harmonic for a closed pipe), the length of the pipe L corresponds to 3λ4, where λ is the wavelength.
2. Determine the Wavelength:
- From the relationship for the first overtone in a closed pipe:
L=3λ4
- Rearranging gives:
λ=4L3
3. Identify the Pressure Amplitude:
- The pressure amplitude P(x) in a closed organ pipe varies as a cosine function due to the phase difference of π2 between displacement and pressure:
P(x)=Pmaxcos(kx)
- Here, k is the wave number given by:
k=2πλ=2π4L3=3π2L
4. Calculate the Pressure Amplitude at Point Q:
- The position of point Q is at x=7L9.
- Substitute x into the pressure amplitude equation:
P(7L9)=Pmaxcos(3π2L⋅7L9)
- Simplifying the argument of the cosine:
P(7L9)=Pmaxcos(3π⋅718)=Pmaxcos(7π6)
5. Evaluate the Cosine:
- The cosine of 7π6 is:
cos(7π6)=−√32
- Therefore, the pressure amplitude at point Q is:
P(7L9)=Pmax(−√32)
6. Find the Ratio:
- The ratio of the pressure amplitude at Q to the maximum pressure amplitude is:
Ratio=P(7L9)Pmax=−√32
- Since we are interested in the magnitude, we take the absolute value:
Ratio=√32
Final Answer:
The ratio of the pressure amplitude at point Q to the maximum pressure amplitude in the pipe is √32.
- A closed organ pipe has one end closed and one end open. In the first overtone (which is the second harmonic for a closed pipe), the length of the pipe L corresponds to 3λ4, where λ is the wavelength.
- From the relationship for the first overtone in a closed pipe:
L=3λ4
- Rearranging gives:
λ=4L3
- The pressure amplitude P(x) in a closed organ pipe varies as a cosine function due to the phase difference of π2 between displacement and pressure:
P(x)=Pmaxcos(kx)
- Here, k is the wave number given by:
k=2πλ=2π4L3=3π2L
- The position of point Q is at x=7L9.
- Substitute x into the pressure amplitude equation:
P(7L9)=Pmaxcos(3π2L⋅7L9)
- Simplifying the argument of the cosine:
P(7L9)=Pmaxcos(3π⋅718)=Pmaxcos(7π6)
- The cosine of 7π6 is:
cos(7π6)=−√32
- Therefore, the pressure amplitude at point Q is:
P(7L9)=Pmax(−√32)
- The ratio of the pressure amplitude at Q to the maximum pressure amplitude is:
Ratio=P(7L9)Pmax=−√32
- Since we are interested in the magnitude, we take the absolute value:
Ratio=√32
The ratio of the pressure amplitude at point Q to the maximum pressure amplitude in the pipe is √32.
Topper's Solved these Questions
Similar Questions
A closed organ pipe of length 1.2 m vibrates in its first overtone mode . The pressue variation is maximum at
View SolutionA closed organ pipe of length L is in resonance with a tuning fork. If a hole is made in the pipe at a distance L4 from closed - end, it will be in resonance again, when:
View SolutionAn open organ pipe of length L vibrates in its fundamental mode. The pressure variation is maximum
View SolutionA string of length 'L' is fixed at both ends . It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance L/3 from one end is
View SolutionA closed organ pipe has length L. The air in it is vibrating in third overtone with maximum amplitude a . The amplitude at distanceL7 from closed of the pipe is a) 0 b) a c) a/2 d) data insufficient
View SolutionAn open organ pipe is vibrating in its fifth overtone. The distance between two consecutive pionts where pressure amlitude is 1√2 times pressure amplitude at pressure antinodes,is 40 cm , then the length of open organ pipe is ( neglect end connection )
View SolutionAn organ pipe open at one end is vibrating in first overtone and is in resonance with another pipe open at both ends and vibrating in third harmonic. The ratio of length of two pipes is–
View SolutionAn open organ pipe of length L vibrates in its second harmonic mode. The correct statement about the Pressure variation is
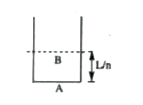
View SolutionA closed organ pipe is vibrating in fundamental frequency. There are two points A and B in the organ pipe as shown, at a distance AB = L/n. Ratio of maximum pressure variation at point A to point B is 2/√3 find value of n
View SolutionIn a closed end pipe of length 105cm , standing waves are set up corresponding to the third overtone . What distance from the closed end, amongst the following is a pressure node?
View Solution
