The acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
41m/s
4m/s
39m/s
27m/s
The correct Answer is:A
To find the velocity of the particle at t=3 seconds given the acceleration function a(t)=3t2+4 and the initial velocity v(0)=2m/s, we can follow these steps:
Step 1: Write down the relationship between acceleration and velocity
Acceleration a(t) is defined as the derivative of velocity v(t) with respect to time t:
a(t)=dvdt
Step 2: Substitute the given acceleration function
We substitute the given acceleration function into the equation:
dvdt=3t2+4
Step 3: Rearrange the equation for integration
We can rearrange the equation to separate variables:
dv=(3t2+4)dt
Step 4: Integrate both sides
Now we integrate both sides. The left side integrates to v and the right side integrates to:
∫dv=∫(3t2+4)dt
This gives us:
v=∫(3t2+4)dt=t3+4t+C
where C is the constant of integration.
Step 5: Determine the constant of integration
To find the constant C, we use the initial condition v(0)=2:
v(0)=03+4(0)+C=2⟹C=2
Thus, the velocity function becomes:
v(t)=t3+4t+2
Step 6: Calculate the velocity at t=3 seconds
Now we substitute t=3 into the velocity function:
v(3)=(3)3+4(3)+2
Calculating this gives:
v(3)=27+12+2=41m/s
Final Answer
The velocity of the particle at t=3 seconds is 41m/s.
Acceleration a(t) is defined as the derivative of velocity v(t) with respect to time t:
a(t)=dvdt
We substitute the given acceleration function into the equation:
dvdt=3t2+4
We can rearrange the equation to separate variables:
dv=(3t2+4)dt
Now we integrate both sides. The left side integrates to v and the right side integrates to:
∫dv=∫(3t2+4)dt
This gives us:
v=∫(3t2+4)dt=t3+4t+C
where C is the constant of integration.
To find the constant C, we use the initial condition v(0)=2:
v(0)=03+4(0)+C=2⟹C=2
Thus, the velocity function becomes:
v(t)=t3+4t+2
Now we substitute t=3 into the velocity function:
v(3)=(3)3+4(3)+2
Calculating this gives:
v(3)=27+12+2=41m/s
The velocity of the particle at t=3 seconds is 41m/s.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.6
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.7
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.4
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
If the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View SolutionAcceleration of a particle at any time t is →a=(2tˆi+3t2ˆj)m/s2.If initially particle is at rest, find the velocity of the particle at time t=2s
View SolutionPower supplied to a particle of mass 3 kg varies with time as p=4t3 watt, where t in time is seconds. If velocity of particle at t=0s is u=2m/s. The velocity of particle at time t=3s will be :
View SolutionPower supplied to a particle of mass 3 kg varies with time as p=4t3 watt, where t in time is seconds. If velocity of particle at t=0s is u=2m/s. The velocity of particle at time t=3s will be :
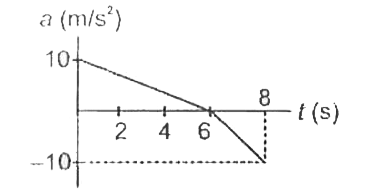
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionPower supplied to a mass 2kg varies with time as P=3t22 watt. Here t is in second . If velocity of particle at t=0isv=0, the velocity of particle at time t=2s will be:
View SolutionThe position of a particle is expressed as →r=(4t2ˆi+2tˆj) m, where t is time in second. Find the velocity o the particle at t = 3 s
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution
