When a mass m is connected individually to two springs and , the oscillation frequencies are and . If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be

The correct Answer is:B
Step by step video & image solution for When a mass m is connected individually to two springs S_(1) and S_(2), the oscillation frequencies are v_(1) and v_(2). If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.34
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.35
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.32
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
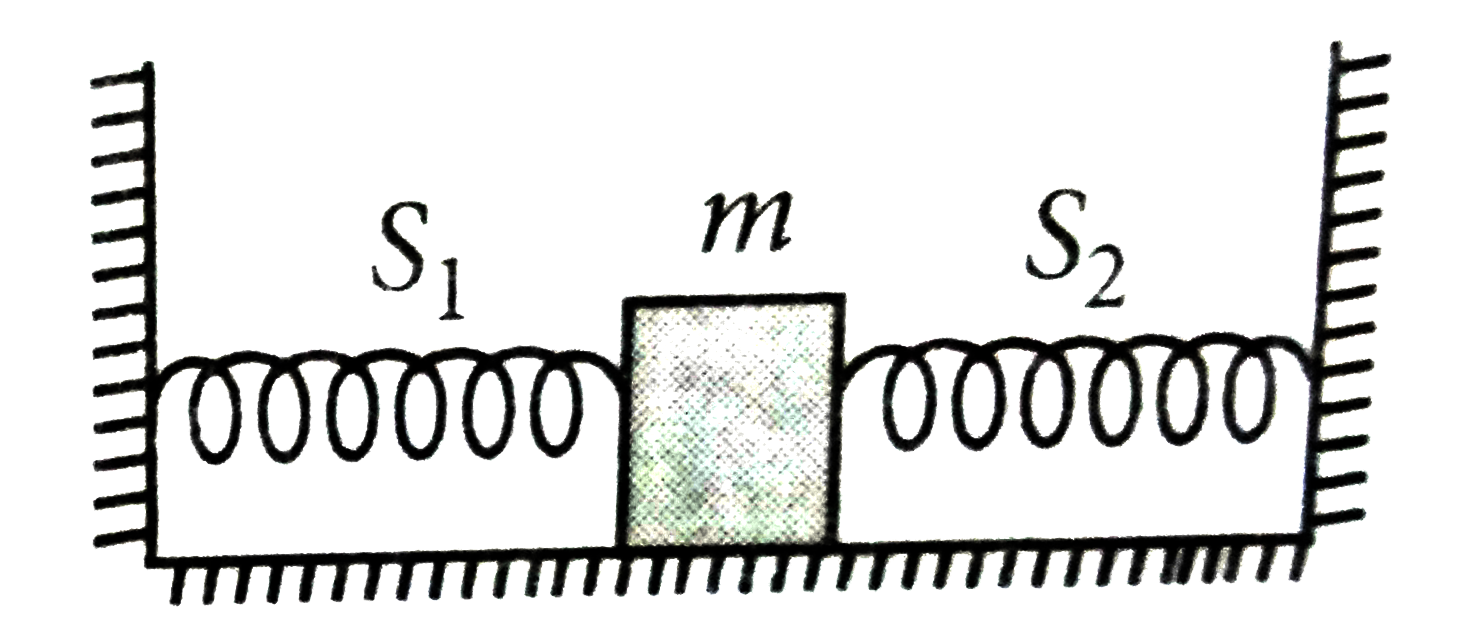
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View Solution
Knowledge Check
When a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
AT=T1+T2B1T=1T1+1T2CT2=T21+T22D1T2=1T21+1T2A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
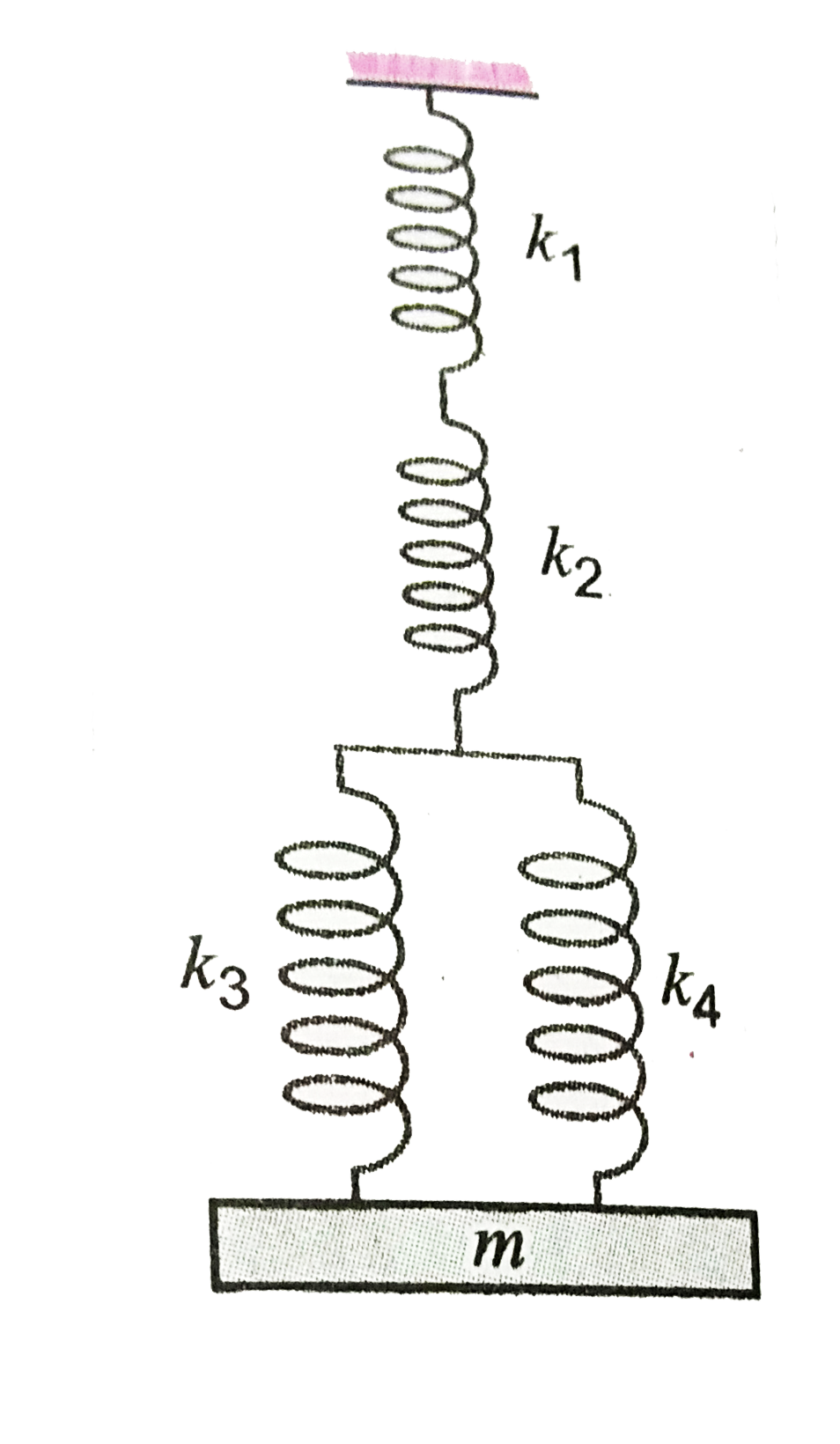 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
Four spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
View SolutionWhen a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
View SolutionThe frequency of oscillation of amass m suspended by a spring is v1. If length of spring is cut to one third then the same mass oscillations with frequency v2. Then
View Solution
