Water is filled to a height in a fixed vertical cylinder placed on horizontal surface. At time t = 0 a small hole I drilled at a height h/4 from bottom of cylinder shown. The cross section area of hole is a and the cross-section area of cyliner is A such that A>>a.

Let the value of horizontal distance of point where the water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t =0 till water comes out of hole, pick the correct statement :
Aa√3h2g
aA√3h2g
Aa√2h3g
None of these
The correct Answer is:A
The initial velocity of water coming out of hole is horizontal and hole is at a height h4 from ground. Hence time taken by water to reach ground is t=√2(h/4)g which remains constant
∴x=vt where v is velocity of effux…
Since v decreases with time x will decrease
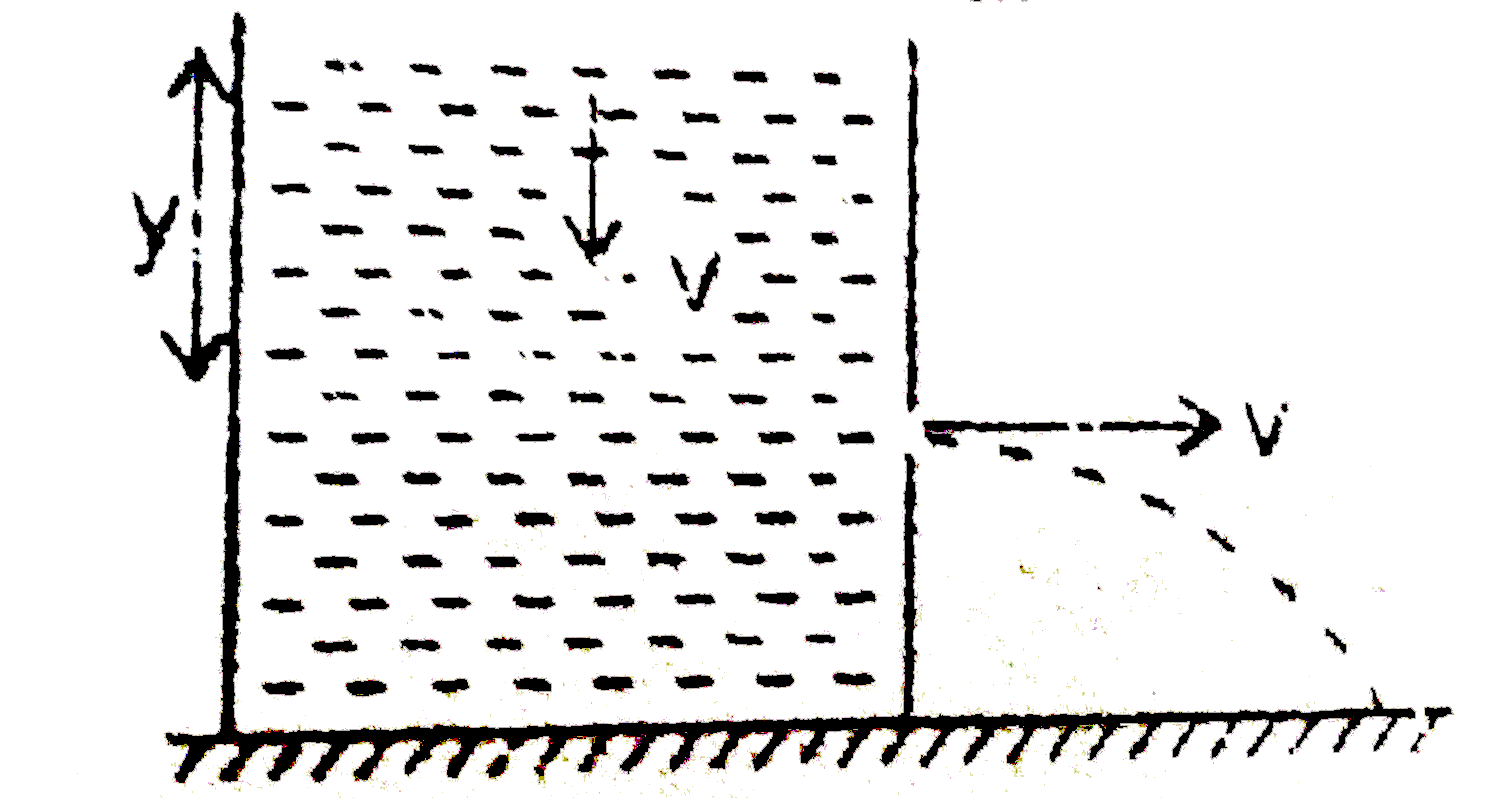
Let y be the height of water surface above hole
∴−dydt=avA=a√2gyA
∴0∫3h/4dy√2gy=t∫0−aAdt
∴t=Aa√3h2g
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.35
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.36
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.33
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Water is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:
View SolutionWater is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

Let the value of horizontal distance of point where the4 water fall on horizontal surface from bottom of cylinder be x as shown. Then from time t=0 till water comes out of hole, pick the correct statement:
View Solution
Knowledge Check
A cylinider is filled with non viscous liquid of density d to a height h0 and a hole is made at a height h1 from the bottom of the cylinder. The velocity issuing out of the hole is
A√2gh0B√2g(h0−h1)C√dgh1D√dgh0
Will the height of the water column change if the cross section of the water column is made wider ?
View Solution_E01_216_Q01.png)
A syringe containing water is held horizontally with its nozzle at a height h above the ground as shown in fig the cross sectional areas of the piston and the nozzle are A and a respectively the piston is pushed with a constant speed v. Find the horizontal range R of the stream of water on the ground.
View SolutionIn a capillary tube , water rises to a height of 4 cm If its cross section area were one forth , the water would have to rises a height of
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionThe given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm, and the other dimensions are as shown. Calculate the total surface area.
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
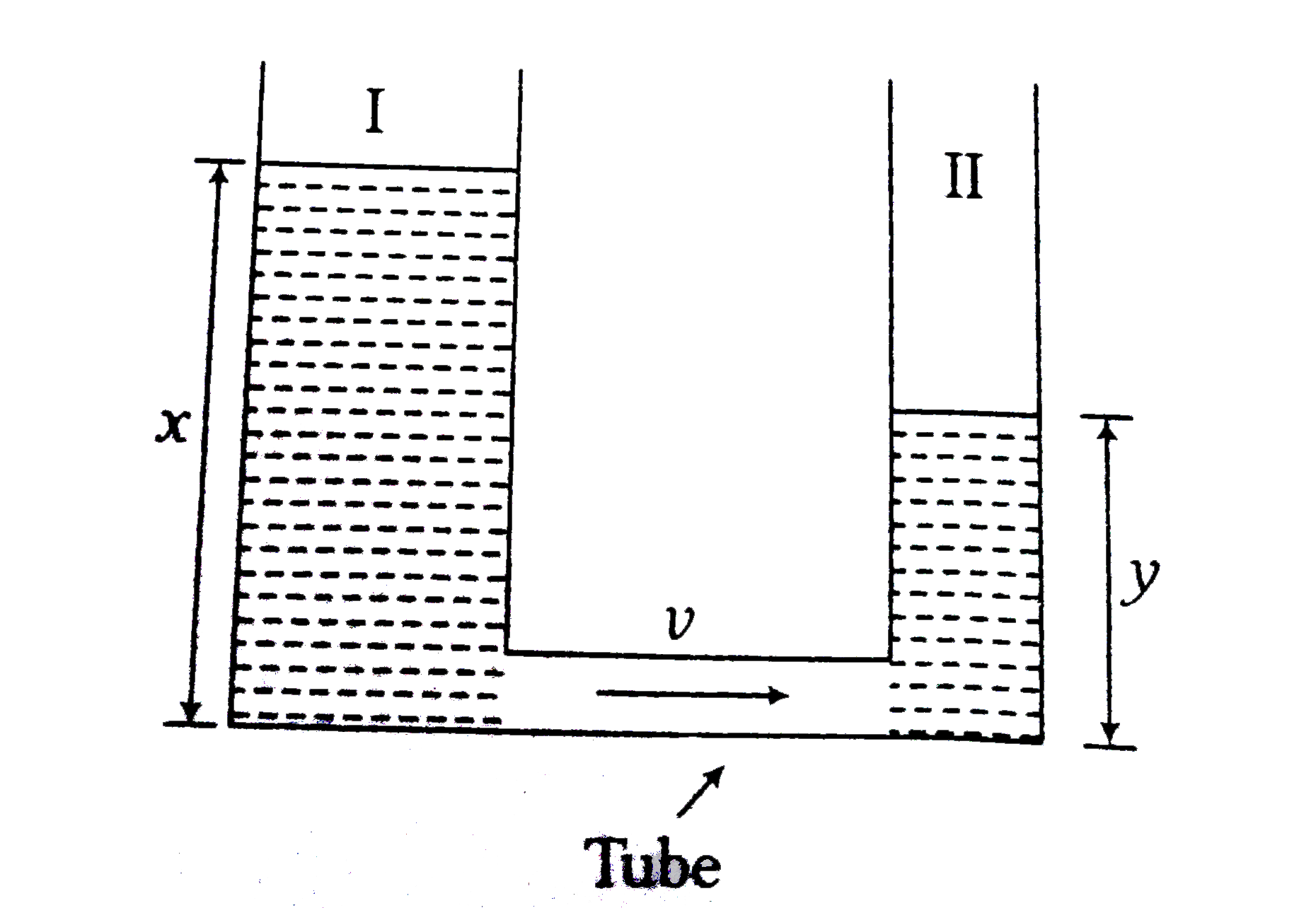
View Solution
