Will the height of the water column change if the cross section of the water column is made wider ?
To determine whether the height of a water column changes when the cross-section of the column is made wider, we can analyze the situation step by step.
Step 1: Understand the Relationship Between Pressure and Height
The pressure at a certain depth in a fluid is given by the formula:
P=ρ⋅g⋅h
where:
- P = pressure,
- ρ = density of the liquid,
- g = acceleration due to gravity,
- h = height of the liquid column.
Step 2: Consider the Effect of Cross-Sectional Area
When the cross-section of the water column is made wider, the area A increases. However, the pressure at a given depth is not dependent on the area of the cross-section. Therefore, the pressure remains constant for a given height of the liquid column.
Step 3: Volume and Height Relationship
The volume V of the liquid column can be expressed as:
V=A⋅h
where A is the cross-sectional area and h is the height of the column. If the area A increases while the volume V remains constant (assuming no liquid is added or removed), the height h must change.
Step 4: Analyze the Change in Height
From the equation V=A⋅h, if A increases, then:
h=VA
This indicates that if the area A increases, the height h must decrease to keep the volume V constant.
Conclusion
Therefore, if the cross-section of the water column is made wider, the height of the water column will decrease.
Summary of Solution
1. Pressure at a depth is given by P=ρ⋅g⋅h.
2. Pressure is independent of the cross-sectional area.
3. Volume of the column is given by V=A⋅h.
4. If the area increases, height must decrease to maintain constant volume.
The pressure at a certain depth in a fluid is given by the formula:
P=ρ⋅g⋅h
where:
- P = pressure,
- ρ = density of the liquid,
- g = acceleration due to gravity,
- h = height of the liquid column.
When the cross-section of the water column is made wider, the area A increases. However, the pressure at a given depth is not dependent on the area of the cross-section. Therefore, the pressure remains constant for a given height of the liquid column.
The volume V of the liquid column can be expressed as:
V=A⋅h
where A is the cross-sectional area and h is the height of the column. If the area A increases while the volume V remains constant (assuming no liquid is added or removed), the height h must change.
From the equation V=A⋅h, if A increases, then:
h=VA
This indicates that if the area A increases, the height h must decrease to keep the volume V constant.
Therefore, if the cross-section of the water column is made wider, the height of the water column will decrease.
1. Pressure at a depth is given by P=ρ⋅g⋅h.
2. Pressure is independent of the cross-sectional area.
3. Volume of the column is given by V=A⋅h.
4. If the area increases, height must decrease to maintain constant volume.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 1 (4 Marks Questions )10videos
FLUIDS
- BOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (2 Marks Questions )45videos
FLUIDS
- BOOK - ICSECHAPTER - FLUIDSEXERCISE - TOPIC 2 (4 Marks Questions )16videos
FLUIDS
- BOOK - ICSECHAPTER - ELECTRICITY AND MAGNETISM EXERCISE - TOPIC 2 Magnetism (4 Marks Questions )6videos
ELECTRICITY AND MAGNETISM
- BOOK - ICSECHAPTER - HEAT AND ENERGYEXERCISE - EXERCISE -6(D) Multiple Choice Question)4videos
HEAT AND ENERGY
Similar Questions
(a) Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6gcm−3
(b) Will the height of the water column in part (a) change if the cross section of the water column is made wider ?View SolutionA capillary tube of radius 0.20 mm is dipped vertically in water. Find the height of the water column raised in the tube. Surface tension of water =0.075Nm−1 and density of water =1000kgm−3.Takeg=10ms−2.
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
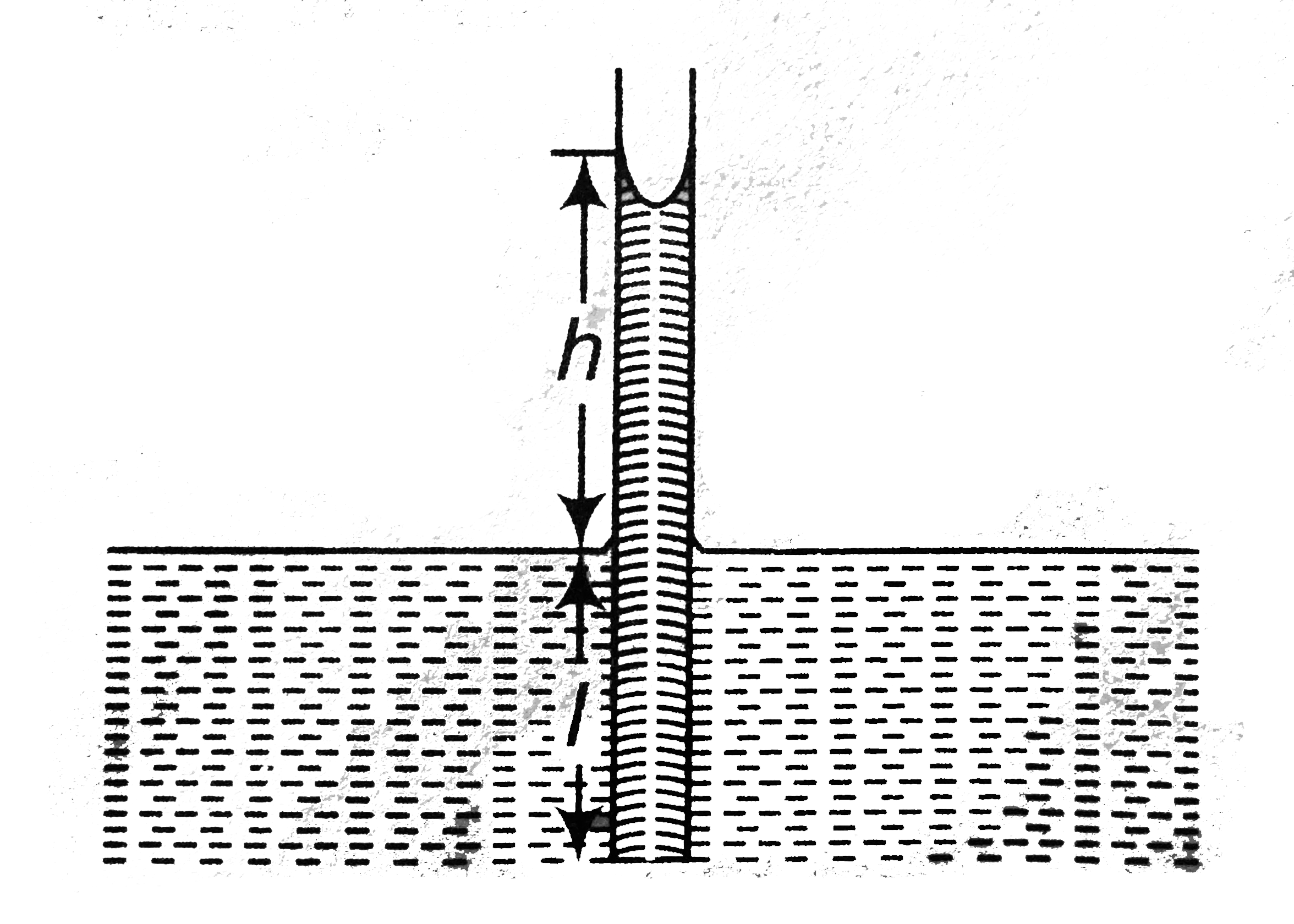 .View Solution
.View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
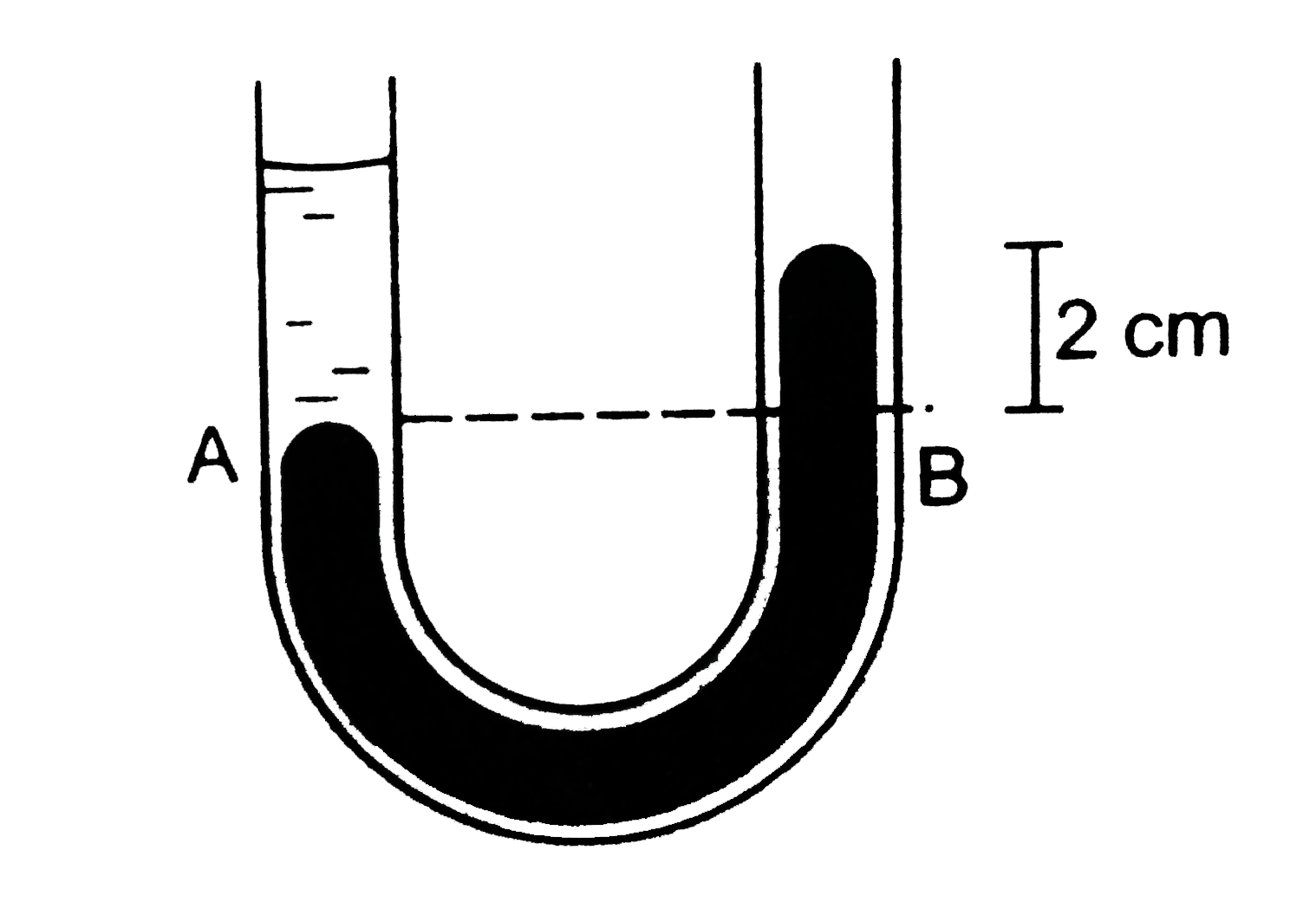 ,View Solution
,View SolutionThe liquids shown in figure in the two arms are mercury (specific gravity =13.6) and water. If the difference of heights of the mercury columns is 2 cm, find the height of the water column.
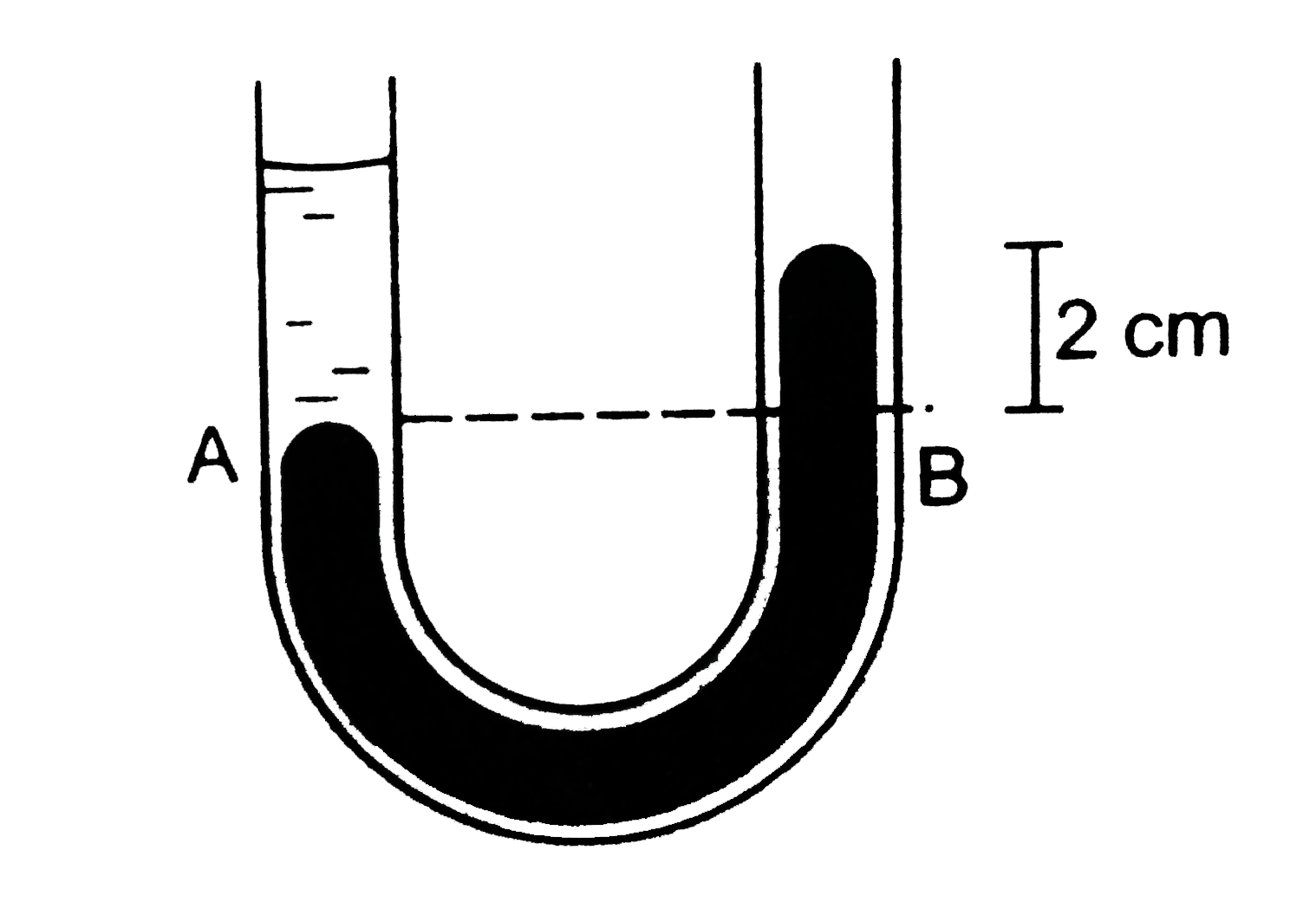 ,View Solution
,View SolutionCalculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. Density of mercury is 13.6g cm−3
View SolutionA vibrating tuning fork is placed over the mouth of a burette filled with water. The tap of the burette is opened and the water level gradually starts falling. It is found that the sound from the tuning fork becomes very loud for a particular length of the water column.
Why does the sound become very loud for this lenght of the water column?View SolutionIn a capillary tube , water rises to a height of 4 cm If its cross section area were one forth , the water would have to rises a height of
View SolutionThe continuity of water column in xylem is maintained due to
View SolutionWater rises to a height of 10cm in a glass capillary tube. If the area of cross section of the tube is reduced to one fourth of the former value what is the height of water rise now?
View Solution

