Current flowing through a conducting wire is given by
I=(1+2t)
Where t is in seconds and current I is in amperes. The charge (in coulombs) flown through the resistor in the interval from t=0 to t=1 second is -
3
2
1
0
The correct Answer is:B
To find the charge flown through the resistor in the interval from t=0 to t=1 second, we start with the given current equation:
I=1+2t
Step 1: Relate current to charge
We know that current I is defined as the rate of flow of charge Q with respect to time t:
I=dQdt
Step 2: Substitute the expression for current
Substituting the expression for I into the equation, we have:
dQdt=1+2t
Step 3: Rearrange the equation
We can rearrange this equation to express dQ:
dQ=(1+2t)dt
Step 4: Integrate both sides
Now, we will integrate both sides. We will integrate dQ from 0 to Q and dt from 0 to 1:
∫Q0dQ=∫10(1+2t)dt
Step 5: Solve the right-hand side integral
Calculating the right-hand side:
∫10(1+2t)dt=∫101dt+∫102tdt
Calculating each part:
1. ∫101dt=(t)10=1−0=1
2. ∫102tdt=(t2)10=12−02=1
Thus, the right-hand side becomes:
1+1=2
Step 6: Set the integrals equal
Now we equate the results of the integrals:
Q=2
Conclusion
The charge flown through the resistor in the interval from t=0 to t=1 second is:
2 Coulombs
---
We know that current I is defined as the rate of flow of charge Q with respect to time t:
Substituting the expression for I into the equation, we have:
We can rearrange this equation to express dQ:
Now, we will integrate both sides. We will integrate dQ from 0 to Q and dt from 0 to 1:
Calculating the right-hand side:
2. ∫102tdt=(t2)10=12−02=1
Now we equate the results of the integrals:
The charge flown through the resistor in the interval from t=0 to t=1 second is:
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.379videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3820videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3520videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)19videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
The current I1 (in A) flowing through the 1Ω resistor in the given circuit is
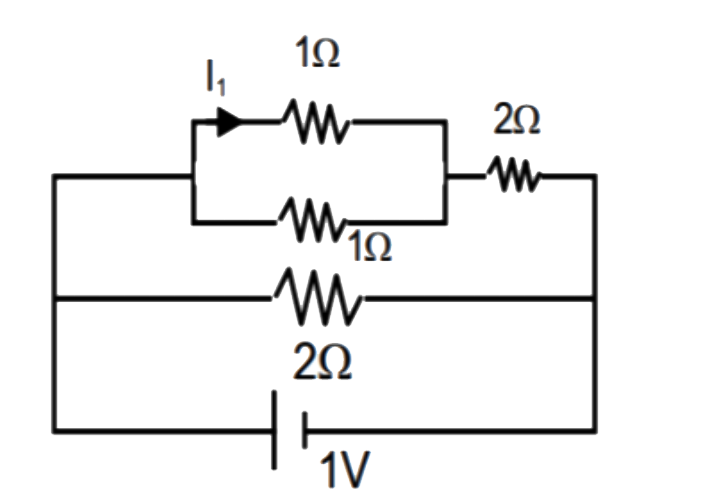 View Solution
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
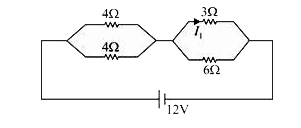 View Solution
View SolutionThe current I1 ( in A ) flowing through 1 Ω resistor in the following circuit is :
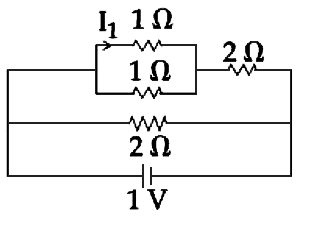 View Solution
View SolutionThe current I1 (in A) flowing through 3Ω resistor in the following circuit is:
 View Solution
View SolutionThe current l through a given cross -section varies with time t as I=3+2t , where l is in ampere and t is in second. The charge passed through this cross-section dring t=0 to t=2 s is
View SolutionThe electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s isView SolutionCharge Q passing through a cross-section of conductor at an instant is given by Q=(0.5t2+t)C where t is in second . Current through the conductor at t=1 is
View SolutionIf the current through an inductor of 2 H is given by I=tsintA, then the voltage across the inductor is
View SolutionThe current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second isView SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View Solution

